
| A. | (0,1] | B. | (0,1) | C. | (1,10) | D. | [1,+∞) |
分析 先求出方程有解的范围,利用补集思想,先求出($\frac{1}{2}$)x=$\frac{1}{1-lga}$没有正根的等价条件即可得到结论.
解答 解:若($\frac{1}{2}$)x=$\frac{1}{1-lga}$有解,则$\frac{1}{1-lga}$>0,则1-lga>0,lga<1,即0<a<10,
若($\frac{1}{2}$)x=$\frac{1}{1-lga}$没有正根,
则x≤0时,方程有解,
∵($\frac{1}{2}$)x≥1,
∴$\frac{1}{1-lga}$≥1,则0<1-lga≤1,
即0≤lga<1,即1≤a<10,
则若关于x的方程($\frac{1}{2}$)x=$\frac{1}{1-lga}$有正根,
则0<a<1,
故选:B
点评 本题主要考查函数与方程的应用,根据指数函数的性质,利用正难则反的原则进行转化是解决本题的关键.


科目:高中数学 来源: 题型:填空题
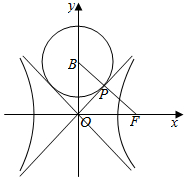 如图,双曲线C:$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1(a,b>0)虚轴上的端点B(0,b),右焦点F,若以B为圆心的圆与C的一条渐近线相切于点P,且$\overrightarrow{BP}$∥$\overrightarrow{PF}$,则该双曲线的离心率为$\frac{1+\sqrt{5}}{2}$.
如图,双曲线C:$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1(a,b>0)虚轴上的端点B(0,b),右焦点F,若以B为圆心的圆与C的一条渐近线相切于点P,且$\overrightarrow{BP}$∥$\overrightarrow{PF}$,则该双曲线的离心率为$\frac{1+\sqrt{5}}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=$±\frac{1}{2}x$ | B. | y=±x | C. | y=±2x | D. | y=±$\sqrt{2}x$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{20}{9}$ | B. | 1 | C. | 2 | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 48 | B. | 24 | C. | 20 | D. | 12 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com