
分析 化简$\frac{a}{x-a}$=$\sqrt{4ax-2{x}^{2}}$=$\sqrt{2{a}^{2}-2(x-a)^{2}}$可得$\frac{{a}^{2}}{(x-a)^{2}}$=2a2-2(x-a)2,从而利用判别式求解.
解答 解:∵$\frac{a}{x-a}$=$\sqrt{4ax-2{x}^{2}}$=$\sqrt{2{a}^{2}-2(x-a)^{2}}$,
∴$\frac{{a}^{2}}{(x-a)^{2}}$=2a2-2(x-a)2,
∴2(x-a)4-2a2(x-a)2+a2=0,
∴△=(-2a2)2-4×2a2≥0,
∴4a2(a2-2)≥0,
故a≥$\sqrt{2}$;
故答案为:[$\sqrt{2}$,+∞).
点评 本题考查了整体思想与转化思想的应用,同时考查了方程的化简与运算及判别式法的应用.


 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案 ABC考王全优卷系列答案
ABC考王全优卷系列答案科目:高中数学 来源: 题型:解答题
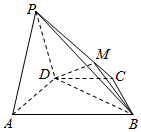 如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,AB∥DC,△PAD是等边三角形,已知BD=2AD=4,$AB=2DC=2\sqrt{5}$.
如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,AB∥DC,△PAD是等边三角形,已知BD=2AD=4,$AB=2DC=2\sqrt{5}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,1] | B. | (0,1) | C. | (1,10) | D. | [1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 假设a,b,c都小于0 | B. | 假设a,b,c中至少有一个不大于0 | ||
| C. | 假设a,b,c中至多有一个不小于0 | D. | 假设a,b,c中至多有一个不大于0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com