
分析 (1)先安排首位的数字,从五个非0数字中选一个,共有C51种结果,余下的五个数字在三个位置进行全排列,共有A53种结果,根据乘法原理得到结果.用0,1,2,3,4,5六个数字组成没有重复数字的四位偶数,则0不能排在首位,末位必须为0,2,4其中之一.属于有限制的排列问题,且限制有两个,即首位和末位,所以,先分两类.第一类,末位排0.第二类,末位不排0,分别求出排法,再相加即可.
(2)当首位是5时,其他几个数字在三个位置上排列,当首位是4时,第二位是5.后两位没有限制,当前两位是43时,分别写出结果数(注意减去4301),相加得到结果,
(3)分别计算,千位,百位,十位,个位,然后相加即可.
解答 解:(1)由题意知,因为数字中有0,0不能放在首位,
∴先安排首位的数字,从五个非0数字中选一个,共有C51种结果,
余下的五个数字在三个位置进行全排列,共有A53种结果,
根据分步计数原理知共有A15•A35=300;
用0,1,2,3,4,5六个数字组成没有重复数字的四位偶数,则0不能排在首位,末位必须为0,2,4其中之一.
所以可分两类,末位为0,则其它位没限制,从剩下的5个数中任取3个,再进行排列即可,共有A53=60个
第二类,末位不排0,又需分步,第一步,从2或4中选一个来排末位,有C21=2种选法,
第二步排首位,首位不能排0,从剩下的4个数中选1个,有4种选法,
第三步,排2,3位,没有限制,从剩下的4个数中任取2个,再进行排列即可,共有12种.
把三步相乘,共有2×4×12=96个
最后,两类相加,共有60+96=156个
(2)当首位是5时,其他几个数字在三个位置上排列,共有A53=60,
当前两位是45时,共有A42=4×3=12个,
当前两位是43时,共有A42=4×3=12个,去掉4301即可,即有12-1=11个.
根据分类加法原理得到共有:60+12+12-1=83个
(3)(1+2+3+4+5)×A53×103+(1+2+3+4+5)×C41A42×(102+10+1)=15×65328=979920
点评 本题是考查排列组合问题,是一个综合题,包括数字问题中可能遇到的所有情况,同学们注意分析问题,加以比较,争取做到举一反三.


 中考解读考点精练系列答案
中考解读考点精练系列答案科目:高中数学 来源: 题型:填空题
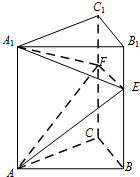 如图,正三棱柱ABC-A1B1C1中,AB=4,AA1=6.若E,F分别是棱BB1,CC1上的点,则三棱锥A-A1EF的体积是8$\sqrt{3}$.
如图,正三棱柱ABC-A1B1C1中,AB=4,AA1=6.若E,F分别是棱BB1,CC1上的点,则三棱锥A-A1EF的体积是8$\sqrt{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{20}{9}$ | B. | 1 | C. | 2 | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
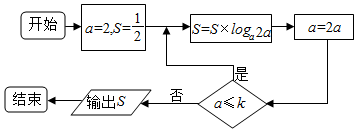
| A. | [16,64] | B. | [16,32) | C. | [32,64) | D. | (32,64) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?x>0,x≤lnx | B. | ?x>0,x<lnx | C. | ?x0>0,x0>lnx0 | D. | ?x0>0,x0≤lnx0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com