
| A. | [$\sqrt{2}$-1,+∞) | B. | [$\sqrt{2}$+1,+∞) | C. | [3-2$\sqrt{2}$,+∞) | D. | [3+2$\sqrt{2}$,+∞) |
分析 先得出M、N横坐标相等,再将恒成立问题转化为求函数的最值问题.
解答 解:由题意,M、N横坐标相等,|$\overrightarrow{MN}$|≤k恒成立,即|$\overrightarrow{MN}$|max≤k,
由N在AB线段上,得A(1,-1),B(2,1),
∴直线AB方程为y=2(x-1)-1
∴|$\overrightarrow{MN}$|=|y1-y2|=|x-$\frac{2}{x}$-2(x-1)+1|=|x+$\frac{2}{x}$-3|,
∵x∈[1,2],∴x+$\frac{2}{x}$∈[2$\sqrt{2}$,3]
∴x+$\frac{2}{x}$-3∈[2$\sqrt{2}$-3,0]
∴|$\overrightarrow{MN}$|max=3-2$\sqrt{2}$
∴k≥3-2$\sqrt{2}$.
故选:C.
点评 本题考查向量知识的运用,考查基本不等式的运用,解答的关键是将已知条件进行转化,同时应注意恒成立问题的处理策略.


 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案科目:高中数学 来源: 题型:解答题
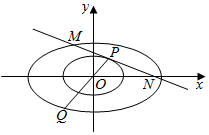 如图,已知椭圆C1:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{1}{2}$,点A(0,$\sqrt{3}$)和点P都在椭圆C1上,椭圆C2方程为$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=4.
如图,已知椭圆C1:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{1}{2}$,点A(0,$\sqrt{3}$)和点P都在椭圆C1上,椭圆C2方程为$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=4.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
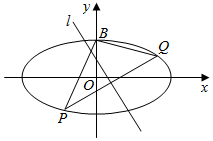 已知中心在原点O,焦点在x轴上的椭圆的一个顶点为B(0,1),B到焦点的距离为2.
已知中心在原点O,焦点在x轴上的椭圆的一个顶点为B(0,1),B到焦点的距离为2.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
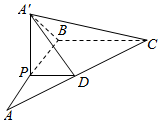 如图,在△ABC中,∠B=$\frac{π}{2}$,AB=BC=2,P为AB上一动点,PD∥BC交AC于点D,现将△PDA沿PD翻折至△PDA′,使平面PDA′⊥平面PBCD.
如图,在△ABC中,∠B=$\frac{π}{2}$,AB=BC=2,P为AB上一动点,PD∥BC交AC于点D,现将△PDA沿PD翻折至△PDA′,使平面PDA′⊥平面PBCD.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com