
分析 (Ⅰ)从袋中随机取两个小球,利用列举法能求出取出的两个小球的编号之和不小于5的概率.
(Ⅱ)先从袋中随机选一个小球,记下编号为m,放回后,再从袋中随机取一个小球,记下编号为n,利用列举法能求出满足条件n=m+2的概率.
解答 解:(Ⅰ)从袋中随机取两个小球,所有可能结果的基本事件为:
{1,2},{1,3},{1,4},{2,3},{2,4},{3,4},共6个,
设“取出的两个小球的编号之和不小于5”为事件A,事件A包含的基本事件为:
{1,4},{2,3},{2,4},{3,4},共4个,
∴所求事件的概率P(A)=$\frac{4}{6}=\frac{2}{3}$.
(Ⅱ)先从袋中随机选一个小球,记下编号为m,放回后,再从袋中随机取一个小球,记下编号为n,
其一切可能的结果记为(m,n),则有:
(1,1),(1,2),(1,3),(1,4),(2,1),(2,2),(2,3),(2,4),
(3,1),(3,2),(3,3),(3,4),(4,1),(4,2),(4,3),(4,4),共16个,
设“满足条件n=m+2”的事件的概率为P(B)=$\frac{2}{16}=\frac{1}{8}$.
点评 本题考查概率的求法,是基础题,解题时要认真审题,注意列举法的合理运用.


科目:高中数学 来源: 题型:选择题
| A. | 2$\sqrt{5}$ | B. | $\sqrt{19}$+$\sqrt{2}$ | C. | 4+$\sqrt{5}$ | D. | 3$\sqrt{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [$\sqrt{2}$-1,+∞) | B. | [$\sqrt{2}$+1,+∞) | C. | [3-2$\sqrt{2}$,+∞) | D. | [3+2$\sqrt{2}$,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\overrightarrow{A{C}_{1}}$ | B. | $\overrightarrow{C{A}_{1}}$ | C. | $\overrightarrow{B{C}_{1}}$ | D. | $\overrightarrow{C{B}_{1}}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
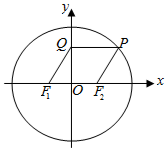 如图,椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的左、右焦点分别为F1,F2,过椭圆上的点P作y轴的垂线,垂足为Q,若四边形F1F2PQ为菱形,则该椭圆的离心率为( )
如图,椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的左、右焦点分别为F1,F2,过椭圆上的点P作y轴的垂线,垂足为Q,若四边形F1F2PQ为菱形,则该椭圆的离心率为( )| A. | $\frac{{\sqrt{2}-1}}{2}$ | B. | $\frac{{\sqrt{3}-1}}{2}$ | C. | $\sqrt{2}-1$ | D. | $\sqrt{3}-1$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com