
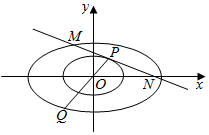
 ��ͼ����֪��ԲC1��$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1��a��b��0����������Ϊ$\frac{1}{2}$����A��0��$\sqrt{3}$���͵�P������ԲC1�ϣ���ԲC2����Ϊ$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=4��
��ͼ����֪��ԲC1��$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1��a��b��0����������Ϊ$\frac{1}{2}$����A��0��$\sqrt{3}$���͵�P������ԲC1�ϣ���ԲC2����Ϊ$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=4������ ��1������Բ�����ʺ͵�P����Բ�ϣ����a��b���ɴ��������ԲC1�ķ��̣�
��2����i����P��m��n��������$\overrightarrow{OQ}$=��$\overrightarrow{OP}$�ã�Q����m����n������P����ԲC1�ϣ�������˵�ֵ��
������l�ķ���Ϊ��y=kx+t������Բ�������ã���4k2+3��x2+8ktx+4t2-12=0���ɴ����ø����б�ʽ��Τ�ﶨ�����ҳ���ʽ���㵽ֱ�߾��빫ʽ����֤����QMN�����Ϊ��ֵ�������ֵΪ18��
��� �⣺��1������ԲC1��$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1��a��b��0����������Ϊ$\frac{1}{2}$����A��0��$\sqrt{3}$���͵�P������ԲC1�ϣ�
��e=$\frac{1}{2}$����a2=4c2=4a2-4b2����3a2=4b2����������֪��b=$\sqrt{3}$����a2=4��
����ԲC1�ķ���Ϊ��$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1$������4�֣�
��2����i����P��m��n��������$\overrightarrow{OQ}$=��$\overrightarrow{OP}$�ã�Q����m����n����
��Q����ԲC2�ϣ���$\frac{{��}^{2}{m}^{2}}{4}+\frac{{��}^{2}{n}^{2}}{3}$=4
��2��$\frac{{m}^{2}}{4}$+$\frac{{n}^{2}}{3}$��=4����P����ԲC1�ϣ���$\frac{{m}^{2}}{4}+\frac{{n}^{2}}{3}$=1�����2=4���֡ߦˣ�0�����=-2������7�֣�
֤������ii��������l�ķ���Ϊ��y=kx+t
���������飺$\left\{\begin{array}{l}{\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1}\\{y=kx+t}\end{array}\right.$����������Ԫ�����ã���4k2+3��x2+8ktx+4t2-12=0��
��=48��4k2+3-t2��=0����4k2+3=t2������
���������飺$\left\{\begin{array}{l}{\frac{{x}^{2}}{16}+\frac{{y}^{2}}{12}=1}\\{y=kx+t}\end{array}\right.$����Ԫ�����ã���16k2+12��x2+32ktx+16t2-16��12=0������
��M��x1��y1����N��x2��y2������x1��x2�Ƿ��̢ٵ������⣬��Τ�ﶨ���ã�
x1+x2=$\frac{-32kt}{16{k}^{2}+12}$��x1x2=$\frac{16{t}^{2}-16��2}{16{k}^{2}+12}$��
|MN|=$\sqrt{1+{k}^{2}}$•$\sqrt{��{x}_{1}+{x}_{2}��^{2}-4{x}_{1}{x}_{2}}$=$\sqrt{1+{k}^{2}}•\frac{16\sqrt{3}•\sqrt{16{k}^{2}+12-{t}^{2}}}{16{k}^{2}+12}$=$\sqrt{1+{k}^{2}}$•$\frac{16\sqrt{3}•\sqrt{12{k}^{2}+9}}{16{k}^{2}+12}$=$\sqrt{1+{k}^{2}}$•$\frac{12}{\sqrt{4{k}^{2}+3}}$��
��O��ֱ��MN�ľ���Ϊd1��Q��ֱ��MN�ľ���Ϊd2�����ɣ�i��֪��d2=3d1
d2=3d1=$\frac{3t}{\sqrt{1+{k}^{2}}}$���ɢ�֪��t=$\sqrt{4{k}^{2}+3}$����d2=$\frac{3\sqrt{4{k}^{2}+3}}{\sqrt{1+{k}^{2}}}$��
��S��QMN=$\frac{1}{2}$•|MN|•d2=$\frac{1}{2}$•$\sqrt{1+{k}^{2}}$•$\frac{12}{\sqrt{4{k}^{2}+3}}$•$\frac{3\sqrt{4{k}^{2}+3}}{\sqrt{1+{k}^{2}}}$=18
����QMN�����Ϊ��ֵ�������ֵΪ18������12�֣�
���� ���⿼����Բ���̵�������ʵ��ֵ�����������������Ϊ��ֵ��֤�������е��⣬����ʱҪ�������⣬ע������б�ʽ��Τ�ﶨ�����ҳ���ʽ���㵽ֱ�߾��빫ʽ�ĺ������ã�


 ������������Ծ�ϵ�д�
������������Ծ�ϵ�д� �������Ӳ�ϵ�д�
�������Ӳ�ϵ�д� ���ɿ��õ�Ԫ����AB��ϵ�д�
���ɿ��õ�Ԫ����AB��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | [$\frac{3}{2}$��+�ޣ� | B�� | [2$\sqrt{2}$-3��+�ޣ� | C�� | [2$\sqrt{2}$-3��$\frac{56}{9}$] | D�� | [$\frac{3}{2}$��$\frac{56}{9}$] |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2$\sqrt{5}$ | B�� | $\sqrt{19}$+$\sqrt{2}$ | C�� | 4+$\sqrt{5}$ | D�� | 3$\sqrt{5}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | [$\sqrt{2}$-1��+�ޣ� | B�� | [$\sqrt{2}$+1��+�ޣ� | C�� | [3-2$\sqrt{2}$��+�ޣ� | D�� | [3+2$\sqrt{2}$��+�ޣ� |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com