
���� ��1��������֪����һ��ȡ5����Ʒ�У�ǡ����k������Ʒ�ĸ���ΪP��k��=${C}_{5}^{k}��\frac{1}{2}��^{5}$���ɴ������������Ʒͨ������ĸ��ʣ�
��2���������X�Ŀ���ȡֵΪ1000��1200��1400���ֱ������Ӧ�ĸ��ʣ��ɴ������X�ķֲ��У�
��� �⣺��1��������֪����һ��ȡ5����Ʒ�У�ǡ����k������Ʒ�ĸ���Ϊ��
P��k��=${C}_{5}^{k}��\frac{1}{2}��^{5}$��k=0��1��2��3��4��5��
��������Ʒͨ������ĸ��ʣ�
p=${C}_{5}^{3}��\frac{1}{2}��^{5}��\frac{1}{2}��^{2}+{C}_{5}^{4}��\frac{1}{2}��^{5}��\frac{1}{2}��+{C}_{5}^{5}��\frac{1}{2}��^{5}$=$\frac{5��4}{2}����\frac{1}{2}��^{7}$+5��$��\frac{1}{2}��^{6}$+��$\frac{1}{2}$��5=$\frac{3}{16}$��
��2���������X�Ŀ���ȡֵΪ1000��1200��1400��
P��X=1000��=��$\frac{1}{2}$��5=$\frac{1}{32}$��
P��X=1200��=${C}_{5}^{4}��\frac{1}{2}��^{6}$=$\frac{5}{64}$��
P��X=1400��=${C}_{5}^{0}��\frac{1}{2}��^{5}+{C}_{5}^{1}��\frac{1}{2}��^{5}$+${C}_{5}^{2}��\frac{1}{2}��^{5}$+${C}_{5}^{3}��\frac{1}{2}��^{5}$=$\frac{57}{64}$��
X�ķֲ���Ϊ��
| X | 1000 | 1200 | 1400 |
| P | $\frac{1}{32}$ | $\frac{5}{64}$ | $\frac{57}{64}$ |
���� ���⿼����ʵ���������ɢ����������ķֲ��е������е��⣬����ʱҪ�������⣬ע��n�ζ����ظ��������¼�Aǡ�÷���k�εĸ��ʼ��㹫ʽ�ĺ������ã�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
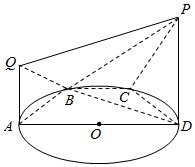 ��ͼ����������ABCD�ĵ�A����60�㣬�����ԲԲ��O�ڱ�AD�ϣ�ֱ������PDAQ��ֱ��ԲO����ƽ�棬��QAD=��PDA=90�㣬��AD=2AQ=4
��ͼ����������ABCD�ĵ�A����60�㣬�����ԲԲ��O�ڱ�AD�ϣ�ֱ������PDAQ��ֱ��ԲO����ƽ�棬��QAD=��PDA=90�㣬��AD=2AQ=4�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
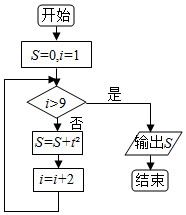 �Ķ���ͼ�ij����ͼ�����ó������к������Sֵ�ǣ�������
�Ķ���ͼ�ij����ͼ�����ó������к������Sֵ�ǣ�������| A�� | 35 | B�� | 63 | C�� | 84 | D�� | 165 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
| ����t���죩 | 3 | 4 | 5 | 6 | 7 |
| ��ֳ����y��ǧ���� | c | 3 | 4 | 4.5 | 6 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{x^2}{16}-\frac{y^2}{9}=1$ | B�� | $\frac{y^2}{16}-\frac{x^2}{9}=1$ | C�� | $\frac{x^2}{9}-\frac{y^2}{16}=1$ | D�� | $\frac{y^2}{9}-\frac{x^2}{16}=1$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��ij�������ɱ��1��2������k��k��N*��k��3��������Բ�����¶�����ɵģ�����ÿһ��Բ���ĸ��������Բ��ֱ����ȣ��Ҷ���������������Բ��������Բ���ĸ�������Բ���ĸߵ�һ�룬����1��Բ���ĸ�Ϊ4��
��ͼ��ij�������ɱ��1��2������k��k��N*��k��3��������Բ�����¶�����ɵģ�����ÿһ��Բ���ĸ��������Բ��ֱ����ȣ��Ҷ���������������Բ��������Բ���ĸ�������Բ���ĸߵ�һ�룬����1��Բ���ĸ�Ϊ4���鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com