
分析 根据题意画出图形,过点A作AM⊥BC,垂足为M,
由此得出当点D在线段MC内时,$\overrightarrow{AD}$•$\overrightarrow{DC}$<0,从而求出对应的概率值.
解答 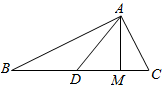 解:如图所示,
解:如图所示,
△ABC中,AB=2,AC=1,∠BAC=120°,
∴BC2=AB2+AC2-2AB•ACcos∠BAC=22+12-2×2×1×cos120°=7,
∴BC=$\sqrt{7}$;
过点A作AM⊥BC,垂足为M,
则$\frac{1}{2}$AM•BC=$\frac{1}{2}$AB•ACsin120°,
∴AM=$\frac{2×1×\frac{\sqrt{3}}{2}}{\sqrt{7}}$=$\frac{\sqrt{3}}{\sqrt{7}}$,
∴BM=$\sqrt{{AB}^{2}{-AM}^{2}}$=$\sqrt{{2}^{2}{-(\frac{\sqrt{3}}{\sqrt{7}})}^{2}}$=$\frac{5}{\sqrt{7}}$;
当点D在线段BM内时,$\overrightarrow{AD}$•$\overrightarrow{DC}$=|$\overrightarrow{AD}$|×|$\overrightarrow{DC}$|×cos∠ADB<0,
故所求的概率为P=$\frac{BM}{BC}$=$\frac{\frac{5}{\sqrt{7}}}{\sqrt{7}}$=$\frac{5}{7}$.
故答案为:$\frac{5}{7}$.
点评 本题考查了平面向量的数量积与几何概型的概率计算问题,也考查了转化法与数形结合思想的应用问题,是基础题目.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
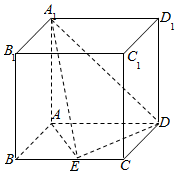 如图,在长方体ABCD-A1B1C1D1中,AA1=$\sqrt{2}$,AB=1,AD=m(m>0),E为BC的中点,且∠A1ED=90°
如图,在长方体ABCD-A1B1C1D1中,AA1=$\sqrt{2}$,AB=1,AD=m(m>0),E为BC的中点,且∠A1ED=90°查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com