
已知函数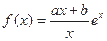 (
( ).
).
(1)若 ,求函数
,求函数 的极值;
的极值;
(2)设 .
.
① 当 时,对任意
时,对任意 ,都有
,都有 成立,求
成立,求 的最大值;
的最大值;
② 设 的导函数.若存在
的导函数.若存在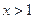 ,使
,使 成立,求
成立,求 的取值范围.
的取值范围.
(1)极大值是e-1,极小值
(2)①-1-e-1 ②(-1,+∞)
【解析】(1)当a=2,b=1时,f (x)=(2+ )ex,定义域为(-∞,0)∪(0,+∞).
)ex,定义域为(-∞,0)∪(0,+∞).
所以f ′(x)= ex
ex
令f ′(x)=0,得x1=-1,x2= ,列表
,列表
x | (-∞,-1) | -1 | (-1,0) | (0, |
| ( |
f ′(x) |
|
| - | - |
|
|
f (x) | ↗ | 极大值 | ↘ | ↘ | 极小值 | ↗ |
由表知f (x)的极大值是f (-1)=e-1,f (x)的极小值是f ( )=
)=
(2)① 因为g (x)=(ax-a)ex-f (x)=(ax- -2a)ex,
-2a)ex,
当a=1时,g (x)=(x- -2)ex.
-2)ex.
因为g (x)≥1在x∈(0,+∞)上恒成立,
所以b≤x2-2x- 在x∈(0,+∞)上恒成立. 记h(x)=x2-2x-
在x∈(0,+∞)上恒成立. 记h(x)=x2-2x- (x>0),则h′(x)=
(x>0),则h′(x)= .
.
当0<x<1时,h′(x)<0,h(x)在(0,1)上是减函数;
当x>1时,h′(x)>0,h(x)在(1,+∞)上是增函数;
所以h(x)min=h(1)=-1-e-1;所以b的最大值为-1-e-1. ②因为g (x)=(ax- -2a)ex,所以g ′(x)=(
-2a)ex,所以g ′(x)=( +ax-
+ax- -a)ex.
-a)ex.
由g (x)+g′(x)=0,得(ax- -2a)ex+(
-2a)ex+( +ax-
+ax- -a)ex=0,
-a)ex=0,
整理得2ax3-3ax2-2bx+b=0.
存在x>1,使g (x)+g ′(x)=0成立.
等价于存在x>1,2ax3-3ax2-2bx+b=0成立.
因为a>0,所以 =
= .
.
设u(x)= (x>1),则u′(x)=
(x>1),则u′(x)= .
.
因为x>1,u′(x)>0恒成立,所以u(x)在(1,+∞)是增函数,所以u(x)>u(1)=-1,
所以 >-1,即
>-1,即 的取值范围为(-1,+∞)
的取值范围为(-1,+∞)


科目:高中数学 来源:2014高考名师推荐数学文空间线面平行、面面平行、线面垂直、面面垂直(解析版) 题型:选择题
设m,n是两条不同的直线,α,β是两个不同的平面,下列命题中正确的是( )
A.若α⊥β,m?α,n?β,则m⊥n
B.若α∥β,m?α,n?β,则m∥n
C.若m⊥n,m?α,n?β,则α⊥β
D.若m⊥α,m∥n,n∥β,则α⊥β
查看答案和解析>>
科目:高中数学 来源:2014高考名师推荐数学文科预测题(解析版) 题型:填空题
如图,AB是⊙O的一条切线,切点为B,ADE、CFD都是⊙O的割线,AC=AB.
(1)证明:AC2=AD·AE
(2)证明:FG∥AC

查看答案和解析>>
科目:高中数学 来源:2014高考名师推荐数学文科预测题(解析版) 题型:解答题
某校高一某班的一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的破坏,其可见部分如下,据此解答如下问题:


(1)计算频率分布直方图中[80,90)间的矩形的高;
(2)若要从分数在 之间的试卷中任取两份分析学生失分情况,求在抽取的试卷中,至少有一份试卷的分数在
之间的试卷中任取两份分析学生失分情况,求在抽取的试卷中,至少有一份试卷的分数在 之间的概率;
之间的概率;
(3)根据频率分布直方图估计这次测试的平均成绩.
查看答案和解析>>
科目:高中数学 来源:2014高考名师推荐数学文科预测题(解析版) 题型:解答题
已知函数f(x)=ex+2x2—3x
(1)求曲线y=f(x)在点(1,f(1))处的切线方程;
(2) 当x ≥1时,若关于x的不等式f(x)≥ax恒成立,求实数a的取值范围;
(3)求证函数f(x)在区间[0,1)上存在唯一的极值点,并用二分法求函数取得极值时相应x的近似值(误差不超过0.2);(参考数据e≈2.7,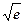 ≈1.6,e0.3≈1.3)。
≈1.6,e0.3≈1.3)。
查看答案和解析>>
科目:高中数学 来源:2014高考名师推荐数学文科解答题前三题(解析版) 题型:解答题
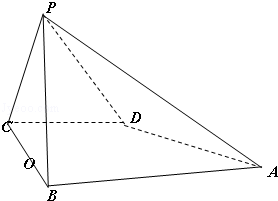
如图,已知四棱锥P﹣ABCD的底面是直角梯形,∠ABC=∠BCD=90°,AB=BC=2CD=2,PB=PC=3,侧面PBC⊥底面ABCD,O是BC的中点.
(1)求证:DC∥平面PAB;
(2)求四棱锥P﹣ABCD的体积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com