Question

17．在平面直角坐标系xOy中，已知点P（0，1）在圆C：x²+y²+2mx-2y+m²-4m+1=0内，若存在过点P的直线交圆C于A、B两点，且△PBC的面积是△PAC的面积的2倍，则实数m的取值范围为（$\frac{4}{9}$，4）．

Answer 1

分析 由点P（0，1）在圆C内，得0＜m＜4，推导出圆心C（-m，1）PB=2PA，设直线l的方程为：y=kx+1．求出圆心C到直线l的距离，从而得到9m²-4m=10d²=10×$\frac{{k}^{2}{m}^{2}}{1+{k}^{2}}$，由此能求出实数m的取值范围．

解答 解：点P（0，1）在圆C：x²+y²+2mx-2y+m²-4m+1=0内，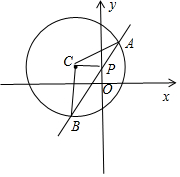
∴1-2+m²-4m+1＜0，
解得0＜m＜4；
又圆C化为标准方程是（x+m）²+（y-1）²=4m，圆心C（-m，1）；
∵△PBC的面积是△PAC的面积的2倍，
∴PB=2PA，
设直线l的方程为：y=kx+1．
圆心C到直线l的距离d=$\frac{|-km-1+1|}{\sqrt{1+{k}^{2}}}$=$\frac{|km|}{\sqrt{1+{k}^{2}}}$．
∴$\sqrt{4m-{d}^{2}}$=3$\sqrt{{m}^{2}-{d}^{2}}$，可得：9m²-4m=10d²=10×$\frac{{k}^{2}{m}^{2}}{1+{k}^{2}}$，
∴9-$\frac{4}{m}$=$\frac{10{k}^{2}}{1+{k}^{2}}$∈（0，10），
解得：$\frac{4}{9}≤m＜4$．
当m=$\frac{4}{9}$时，四点共线没有三角形，
∴实数m的取值范围为（$\frac{4}{9}$，4）．
故答案为：（$\frac{4}{9}$，4）．

点评 本题考查实数的取值范围的求法，考查圆的方程、点到直线距离公式等基础知识，考查推理论证能力、运算求解能力，考查化归与转化思想、函数与方程思想，是中档题．