
| A. | y=sin|x| | B. | y=sin2x | C. | y=-sinx+2 | D. | y=sinx+1 |
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [0,2] | B. | [1-$\frac{\sqrt{2}}{2}$,2] | C. | [0,1-$\frac{\sqrt{2}}{2}$] | D. | [0,1+$\frac{\sqrt{2}}{2}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 第十届珠海航展与10月28日至11月1日在珠海市机场路航展馆举行,组委会为了做好接待工作,对参加服务的200名工作人员进行为期一周的培训,培训结束对服务人员进行珠海航展知识测评,其成绩的频率分布直方图如图所示,规定95分及其以上获优胜奖.
第十届珠海航展与10月28日至11月1日在珠海市机场路航展馆举行,组委会为了做好接待工作,对参加服务的200名工作人员进行为期一周的培训,培训结束对服务人员进行珠海航展知识测评,其成绩的频率分布直方图如图所示,规定95分及其以上获优胜奖.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
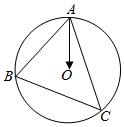
| A. | 6 | B. | 10 | C. | 16 | D. | 20 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com