
分析 由向量共线的条件判断①;由函数解析式求出$f(-\frac{π}{6})=0$判断②;结合(0,$\frac{π}{2}$)内tanx>x>sinx判断③;由三角形中大边对大角及正弦定理判断④;由函数y=Acos(ωx+φ)(A>0,ω>0)为奇函数,可知当x=0时相位的终边落在y轴上,求出φ值判断⑤.
解答 解:①,若非零向量$\overrightarrow a$,$\overrightarrow b$满足|${\overrightarrow a$-$\overrightarrow b$|=|${\overrightarrow a}$|+|${\overrightarrow b}$|,则$\overrightarrow{a},\overrightarrow{b}$共线反向,存在实数λ<0,使得$\overrightarrow b$=λ$\overrightarrow a$,故①错误;
②,∵$f(-\frac{π}{6})=4cos[2×(-\frac{π}{6})-\frac{π}{6}]=0$,∴函数 f(x)=4cos(2x-$\frac{π}{6}$)的图象关于点(-$\frac{π}{6}$,0)对称,故②正确;
③,∵在(0,$\frac{π}{2}$)内tanx>x,在($-\frac{π}{2}$,0)内tanx<x,而x=sinx在(-$\frac{π}{2}$,$\frac{π}{2}$)内有唯一解0,∴方程 tanx=sinx在(-$\frac{π}{2}$,$\frac{π}{2}$)内有唯一解0,故③错误;
④,在△ABC中,A>B?a>b,再由正弦定理可得,a>b?sinA>sinB,∴A>B?sinA>sinB,故④正确;
⑤,若函数y=Acos(ωx+φ)(A>0,ω>0)为奇函数,则ω×0+φ=kπ+$\frac{π}{2}$(k∈Z),即φ=kπ+$\frac{π}{2}$(k∈Z),故⑤正确.
∴正确命题的序号为②④⑤.
故答案为:②④⑤.
点评 本题考查命题的真假判断与应用,考查了共线向量的概念,考查三角函数的图象和性质,是中档题.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{2}}{2}$ | B. | $\frac{1}{2}$ | C. | $\frac{\sqrt{2}}{4}$ | D. | $\frac{1}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {-1,0,1} | B. | {0,1,2} | C. | {0,1} | D. | {1,2} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
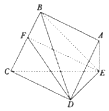 如图所示,边长为2的正方形ABCD所在的平面与△CDE所在的平面交于CD,且AE⊥平面CDE,AE=1.
如图所示,边长为2的正方形ABCD所在的平面与△CDE所在的平面交于CD,且AE⊥平面CDE,AE=1.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(a)<$\frac{f(0)}{{e}^{ax}}$ | B. | f(a)>$\frac{f(0)}{{e}^{a}}$ | C. | f(a)<eaf(0) | D. | f(a)>eaf(0) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com