
分析 根据已知分析出函数的周期性,结合当x∈(-2,0]时,f(x)=x+1,画出当2<x≤4时,函数的图象,再由$\frac{f(x)}{x}$的几何意义得到答案.
解答 解:∵f(x)对任意的x∈R,都有f(x-1)=f(x+1),
∴函数f(x)是以2为周期的周期函数,
又∵当x∈(-2,0]时,f(x)=x+1,
∴函数f(x)的图象如下图所示: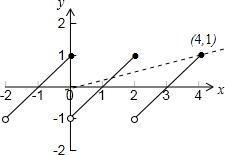
$\frac{f(x)}{x}$表示函数f(x)图象上的点与原点连线的斜率,
故当2<x≤4时,$\frac{f(x)}{x}$的最大值为$\frac{1}{4}$,
故答案为:$\frac{1}{4}$
点评 本题考查的知识点是函数的周期性,斜率公式,正确理解$\frac{f(x)}{x}$的几何意义是解答的关键.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
| A. | 充分而不必要条件 | B. | 必要而充分不条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $x=-\frac{π}{12}$ | B. | $x=-\frac{π}{6}$ | C. | $x=\frac{π}{6}$ | D. | $x=\frac{π}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,0) | B. | (0,+∞) | C. | (-∞,0)∪(0,+∞) | D. | (-∞,+∞) |
查看答案和解析>>
科目:高中数学 来源:2017届河北正定中学高三上月考一数学(理)试卷(解析版) 题型:选择题
设点 和点
和点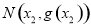 分别是函数
分别是函数 和
和 图象上的点,且
图象上的点,且 ,若直线
,若直线 轴,则
轴,则 两点间的距离的最小值为( )
两点间的距离的最小值为( )
A.1 B.2 C.3 D.4
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|0<x<1} | B. | {x|0≤x<1} | C. | {x|-1<x≤1} | D. | {x|-2<x≤1} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com