
| A. | $\frac{5}{12}$ | B. | $\frac{5}{18}$ | C. | $\frac{5}{6}$ | D. | $\frac{5}{36}$ |
分析 先求出基本事件总数,再由列举法求出直线ax-y+a-b=0在y轴上截距大于在x轴上截距的基本事件个数,由此能求出线ax-y+a-b=0在y轴上截距大于在x轴上截距的概率.
解答 解:∵掷两枚质地均匀的骰子,其向上的点数分别记为a,b,
∴基本事件总数n=6×6=36,
∵直线ax-y+a-b=0在y轴上截距大于在x轴上截距,
∴a-b>$\frac{b}{a}$-1,
∴满足条件的基本事件有:
(2,1),(3,1),(3,2),(4,1),(4,2),(4,3),(5,1),(5,2),(5,3),(5,4),(6,1),(6,2),(6,3),(6,4),(6,5),共15个,
∴直线ax-y+a-b=0在y轴上截距大于在x轴上截距的概率:
p=$\frac{15}{36}=\frac{5}{12}$.
故选:A.
点评 本题考查概率的求法,是基础题,解题时要认真审题,注意等可能事件概率计算公式的合理运用.


科目:高中数学 来源: 题型:解答题
| 房号/户型 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| A户型 | 0.98 | 0.99 | 1.06 | 1.17 | 1.10 | 1.21 | a | 1.09 | 1.14 |
| B户型 | 1.08 | 1.11 | 1.12 | b | 1.26 | 1.27 | 1.26 | 1.25 | 1.28 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 编号 | 1 | 2 | 3 | 4 | 5 |
| x | 169 | 178 | 166 | 175 | 180 |
| y | 75 | 80 | 77 | 70 | 81 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 最大值为1,图象关于直线x=$\frac{π}{2}$对称 | B. | 在(0,$\frac{π}{4}$)上单调递减,为奇函数 | ||
| C. | 在(-$\frac{3π}{8}$,$\frac{π}{8}$)上单调递增,为偶函数 | D. | 周期为π,图象关于点($\frac{3π}{8}$,0)对称 |
查看答案和解析>>
科目:高中数学 来源:2016-2017学年广东清远三中高二上学期第一次月考数学(理)试卷(解析版) 题型:解答题
已知函数 .
.
(Ⅰ)求 的值域;
的值域;
(Ⅱ)设△ 的内角A、B、C所对的边分别为a、b、c,已知
的内角A、B、C所对的边分别为a、b、c,已知 为锐角,
为锐角,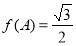 ,
, ,
, ,求
,求 的值.
的值.
查看答案和解析>>
科目:高中数学 来源:2016-2017学年广东清远三中高二上学期第一次月考数学(理)试卷(解析版) 题型:解答题
设有关于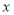 的一元二次方程
的一元二次方程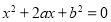 .
.
(Ⅰ)若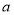 是从
是从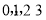 四个数中任取的一个数,
四个数中任取的一个数,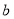 是从
是从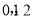 三个数中任取的一个数,求上述方程有实根的概率;
三个数中任取的一个数,求上述方程有实根的概率;
(Ⅱ)若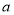 是从区间
是从区间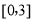 任取的一个数,
任取的一个数,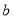 是从区间
是从区间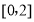 任取的一个数,求上述方程有实根的概率.
任取的一个数,求上述方程有实根的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com