
分析 {an}是斐波那契数列,求得{an}中各项除以3所得余数组成以8为周期的周期数列,各项除以4所得余数组成以6为周期的周期数列,从而可得结论.
解答 解:依题意,该数列为:1,1,2,3,5,8,13,21,34,55,89,144,…
各项依次除以3所得的余数记为数列{bn},则为1,1,2,0,2,2,1,0,1,1,2,0,…,即{cn}中各项除以3所得余数组成以8为周期的周期数列,
而2016=252×8,故b2016=0
除以4所得的余数记为数列{cn},则1,1,2,3,1,0,1,1,2,3,1,0,…即{cn}中各项除以4所得余数组成以6为周期的周期数列,
而2016=336×6,故C2016=0,
故b2016+c2016=0,
故答案为:0.
点评 本题考查了斐波那契数列,以及周期数列,考查了学生的分析问题解决问题的能力,属于中档题.


 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案科目:高中数学 来源: 题型:选择题
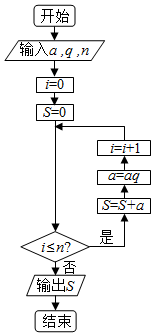
| A. | a+aq+…+aqn-1 | B. | $\frac{{a(1-{q^n})}}{1-q}$ | C. | a+aq+…+aqn | D. | $\frac{{a(1-{q^{n+1}})}}{1-q}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [2,4] | B. | [$\frac{5}{6}$,$\frac{11}{6}$] | C. | [$\frac{5}{6}$,2] | D. | [1,2] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | 0 | D. | 0或-$\frac{1}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com