
分析 由两个向量平行得到m=y2+x2,即求区域内点到原点距离的最小值,利用数形结合可求.
解答  解:由已知约束条件得到可行域如图:向量$\overrightarrow{a}$=(y2+x2,m),$\overrightarrow{b}$=(1,1),且$\overrightarrow{a}∥\overrightarrow{b}$,则m=x2+y2,m的最小值为图中M(1,$\frac{1}{2}$)到原点距离的平方,
解:由已知约束条件得到可行域如图:向量$\overrightarrow{a}$=(y2+x2,m),$\overrightarrow{b}$=(1,1),且$\overrightarrow{a}∥\overrightarrow{b}$,则m=x2+y2,m的最小值为图中M(1,$\frac{1}{2}$)到原点距离的平方,
所以m的最小值为12+$(\frac{1}{2})^{2}$=$\frac{5}{4}$;
故答案为:$\frac{5}{4}$.
点评 本题考查了简单线性规划问题;利用数形结合是解答的关键.


 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案科目:高中数学 来源: 题型:选择题
| A. | {0,1,2,4} | B. | {0,1,2} | C. | {1,4} | D. | {0,1,4} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 2$\sqrt{2}$ | C. | 4 | D. | 2$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
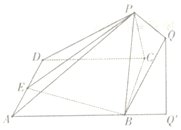 已知如图所示的几何体中,四边形ABCD是边长为2的菱形,面PBC⊥面A BCD,点E是AD 的中点,PQ∥面ABCD且点Q在面ABCD上的射影Q′落在AB的延长线上,若PQ=1,PB=$\sqrt{2}$,且($\overrightarrow{PB}+\overrightarrow{PC}$)•$\overrightarrow{BC}$=0,$\overrightarrow{AB}•\overrightarrow{AD}$=2
已知如图所示的几何体中,四边形ABCD是边长为2的菱形,面PBC⊥面A BCD,点E是AD 的中点,PQ∥面ABCD且点Q在面ABCD上的射影Q′落在AB的延长线上,若PQ=1,PB=$\sqrt{2}$,且($\overrightarrow{PB}+\overrightarrow{PC}$)•$\overrightarrow{BC}$=0,$\overrightarrow{AB}•\overrightarrow{AD}$=2查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | 1 | D. | 0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在多面体ABCDEF中,正三角形BCE所在平面与菱形ABCD所在的平面垂直,FD⊥平面ABCD,且$BC=4,FD=2\sqrt{3}$.
如图,在多面体ABCDEF中,正三角形BCE所在平面与菱形ABCD所在的平面垂直,FD⊥平面ABCD,且$BC=4,FD=2\sqrt{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2$\sqrt{5}$ | B. | 10 | C. | 12 | D. | 8 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com