
| A�� | 2$\sqrt{5}$ | B�� | 10 | C�� | 12 | D�� | 8 |
���� ������������������ƽ�����������������������ļ������弴����$\overrightarrow{a}$�ϵ�ͶӰ�ж�AB�����λ�ã����ɵõ�����
��� 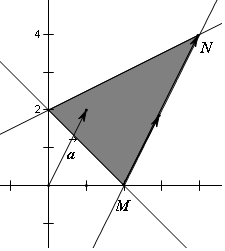 �⣺ƽ������$\left\{\begin{array}{l}{2x-y-4��0}\\{x-2y+4��0}\\{x+y-2��0}\end{array}\right.$�Ŀ�������ͼ��ƽ��$\overrightarrow{a}$���������M��
�⣺ƽ������$\left\{\begin{array}{l}{2x-y-4��0}\\{x-2y+4��0}\\{x+y-2��0}\end{array}\right.$�Ŀ�������ͼ��ƽ��$\overrightarrow{a}$���������M��
�ɿ������֪��$\overrightarrow{MN}•\overrightarrow{a}$�����ֵ����$\overrightarrow{MN}$��$\overrightarrow{a}$�ϵ�ͶӰȡ�����ֵ��
��$\left\{\begin{array}{l}{2x-y-4=0}\\{x+y-2=0}\end{array}\right.$�ɵ�M��2��0������$\left\{\begin{array}{l}{2x-y-4=0}\\{x-2y+4=0}\end{array}\right.$�õ�N��4��4����$\overrightarrow{MN}$=��2��4����
��ʱ$\overrightarrow{MN}$•$\overrightarrow{a}$=1��2+2��4=10��
��ѡ��B��
���� ���⿼�����Թ滮�������������ʾ��ƽ�������������ļ�������Ȼ���֪ʶ���������ν�ϵ���ѧ˼�룬�����е��⣮


 ��˼ά������ҵ��ټ��ִ�ѧ������ϵ�д�
��˼ά������ҵ��ټ��ִ�ѧ������ϵ�д� �����������Ż�ѧϰϵ�д�
�����������Ż�ѧϰϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 6 | B�� | 9 | C�� | 10 | D�� | 12 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
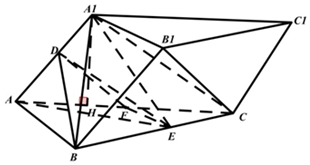 ��ͼ��������ABC-A1B1C1�У�����ACC1A1�͵���ABC����A1AC=60�㣬AC=2AA1=4����D��E�ֱ���AA1��BC���е㣮
��ͼ��������ABC-A1B1C1�У�����ACC1A1�͵���ABC����A1AC=60�㣬AC=2AA1=4����D��E�ֱ���AA1��BC���е㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1 | B�� | -1 | C�� | -i | D�� | i |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��ַDZ�Ҫ���� | B�� | ��Ҫ�dz������ | ||
| C�� | ��Ҫ���� | D�� | �ȷdz���ַDZ�Ҫ���� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ����t��R��ʹf��x����2��[t-$\frac{1}{2}$��t+$\frac{1}{2}$]�Ϻ���� | |
| B�� | ����t��R��ʹ0��f��x����2��[t-$\frac{1}{2}$��t+$\frac{1}{2}$]�Ϻ���� | |
| C�� | ����t��R��ʹf��x����[t-$\frac{1}{2}$��t+$\frac{1}{2}$]��ʼ�մ��ڷ����� | |
| D�� | ����t��R+��ʹf��x����[t-$\frac{1}{2}$��t+$\frac{1}{2}$]��ʼ�մ��ڷ����� |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com