
| A. | 存在t∈R,使f(x)≥2在[t-$\frac{1}{2}$,t+$\frac{1}{2}$]上恒成立 | |
| B. | 存在t∈R,使0≤f(x)≤2在[t-$\frac{1}{2}$,t+$\frac{1}{2}$]上恒成立 | |
| C. | 存在t∈R,使f(x)在[t-$\frac{1}{2}$,t+$\frac{1}{2}$]上始终存在反函数 | |
| D. | 存在t∈R+,使f(x)在[t-$\frac{1}{2}$,t+$\frac{1}{2}$]上始终存在反函数 |
分析 利用对称性作出f(x)的函数图象,根据图象即可判断出结论.
解答 解:∵f(1+x)=f(1-x),∴f(x)关于直线x=1对称,
作出f(x)的函数图象如图所示: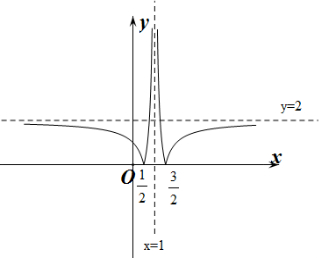
由图象可知f(x)≥2的解集为($\frac{3}{4}$,1)∪(1,$\frac{5}{4}$),
∴不存在一个长度为1的区间[t-$\frac{1}{2}$,t+$\frac{1}{2}$]使得f(x)≥2恒成立,故A错误,
由图象可知0≤f(x)≤2的解集为(-∞,$\frac{3}{4}$)∪($\frac{5}{4}$,+∞),
∴存在一个长度为1的区间[t-$\frac{1}{2}$,t+$\frac{1}{2}$]使得0≤f(x)≤2在[t-$\frac{1}{2}$,t+$\frac{1}{2}$]上恒成立,故B正确;
由图象可知f(x)在(-∞,$\frac{1}{2}$)和($\frac{1}{2}$,+∞)上为单调函数,
∴存在某个区间[t-$\frac{1}{2}$,t$+\frac{1}{2}$]⊆(-∞,$\frac{1}{2}$)∪($\frac{1}{2}$,+∞),使得f(x)在此区间上存在反函数,
故C,D正确;
故选A.
点评 本题考查了函数的对称性判断,函数具有反函数的条件,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 2$\sqrt{5}$ | B. | 10 | C. | 12 | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
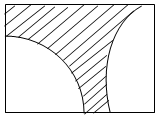 已知矩形的长为10,宽为5(如图所示),在矩形内随机地投掷1000颗黄豆,数得落在阴影部分的黄豆为560颗,则可以估计阴影部分的面积为2.8.
已知矩形的长为10,宽为5(如图所示),在矩形内随机地投掷1000颗黄豆,数得落在阴影部分的黄豆为560颗,则可以估计阴影部分的面积为2.8.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 数学尖子生 | 数学尖子生 | 合计 | |
| 男生 | |||
| 女生 | |||
| 合计 | 100 |
| P(K2≥k2) | 0.15 | 0.10 | 0.05 | 0.025 | 0.01 | 0.005 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com