
分析 (1)求出函数的导数,判断出导函数的符号,从而求出函数的单调性;
(2)讨论a的范围,得到函数的单调区间,从而表示出函数在闭区间上的最小值,求出a的值即可;
(3)法一:令函数h(x)=(x-1)-lnx(x>0),求出函数的导数,根据函数的单调性证明即可;法二:分离参数证明即可.
解答 解:(1)由题设易知f(x)=lnx,∴g(x)=lnx+$\frac{a}{x}$,g(x)的定义域为(0,+∞),
且g′(x)=$\frac{1}{x}-\frac{a}{x^2}=\frac{x-a}{x^2}$.∵a<0,∴g′(x)>0,
故g(x)在(0,+∞)上是单调递增函数.…(3分)
(2)①若a≤1,则x-a≥0,即f′(x)≥0在[1,e]上恒成立,
此时g(x)在[1,e]上为增函数,
∴g(x)min=g(1)=a=$\frac{3}{2}$>1 (舍去).
②若a≥e,则x-a≤0,则g′(x)≤0在[1,e]上恒成立,
此时g(x)在[1,e]上为减函数,
∴g(x)min=g(e)=1+$\frac{a}{e}$=$\frac{3}{2}$,∴a=$\frac{e}{2}$<e (舍去).
③若1<a<e,令g′(x)=0得x=a,
当1<x<a时,g′(x)<0,∴f(x)在(1,a)上为减函数;
当a<x<e时,g′(x)>0,∴f(x)在(a,e)上为增函数,
∴g(x)min=g(a)=lna+1=$\frac{3}{2}$,∴a=$\sqrt{e}$.
综上所述,a=$\sqrt{e}$.…(8分)
(3)令函数h(x)=(x-1)-lnx(x>0),
$则h'(x)=1-\frac{1}{x}=\frac{x-1}{x}$x>1时,h′(x)>0,又在x=1处连续,
∴x∈[1,+∞)时,为增函数,∵$1+\frac{1}{x}>1$,
∴$h({1+\frac{1}{x}})>h(1)=0$,即:$\frac{1}{x}-ln({1+\frac{1}{x}})>0$,
整理得:$\frac{1}{x}+lnx>ln({x+1})$,
又当a≥1时,有$g(x)≥\frac{1}{x}+lnx>ln({x+1})$,命题得证.…(12分)
法二:可探究“g(x)>ln(x+1)在(0,+∞)上恒成立”的充要条件是“a≥1”.
由g(x)>ln(x+1)得:$a>xln({1+\frac{1}{x}})$,令$h(x)=xln({1+\frac{1}{x}}),x∈({0,+∞})$,
利用导数与极限知识,可求h(x)的最大值.
点评 本题考查了函数的单调性、最值问题,考查导数的应用以及函数恒成立问题,是一道综合题.


 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | 0.2 | B. | 0.5 | C. | 0.75 | D. | 1.5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-e,e) | B. | (-∞,-e)∪(e,+∞) | C. | (-∞,-e)∪(0,e) | D. | (-e,0)∪(e,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
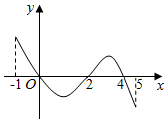 已知函数f(x)的定义域为[-1,5],部分对应值如表,f(x)的导函数y=f′(x)的图象如图所示,
已知函数f(x)的定义域为[-1,5],部分对应值如表,f(x)的导函数y=f′(x)的图象如图所示,| x | -1 | 0 | 2 | 4 | 5 |
| f(x) | 1 | 2 | 1.5 | 2 | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com