

| A. | 2 | B. | 4 | C. | 6 | D. | 8 |
分析 由$(1-x)sinπx=\frac{1}{2}$,得2sinπx=$\frac{1}{1-x}$,设y=2sinπx和y=$\frac{1}{1-x}$,作出两个函数的图象,利用函数的对称性进行求解即可.
解答  解:由$(1-x)sinπx=\frac{1}{2}$,得2sinπx=$\frac{1}{1-x}$,
解:由$(1-x)sinπx=\frac{1}{2}$,得2sinπx=$\frac{1}{1-x}$,
设y=2sinπx和y=$\frac{1}{1-x}$,作出两个函数的图象,
则两个函数都关于点(1,0)对称,
由图象可知两个函数共有8个交点,它们两两关于点(1,0)对称,
不妨设关于x对称的两个零点的横坐标分别为x1,x2,
则$\frac{{x}_{1}+{x}_{2}}{2}=1$,
即x1+x2=2,
∴所有8个零点之和为4(x1+x2)=4×2=8,
故选:D
点评 本题主要考查函数零点的应用,利用数形结合将函数转化为两个函数的交点问题,结合函数的对称性是解决本题的关键.综合考查函数的性质.


科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{3}$ | B. | $\sqrt{6}$ | C. | 3 | D. | 2$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
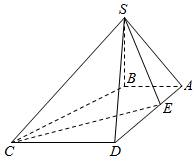 如图,在四棱锥S-ABCD中,SB⊥底面ABCD,底面ABCD为梯形,AB⊥AD,AB∥CD,AB=1,AD=3,CD=2.若点E是线段AD上的动点,则满足∠SEC=90°的点E的个数是( )
如图,在四棱锥S-ABCD中,SB⊥底面ABCD,底面ABCD为梯形,AB⊥AD,AB∥CD,AB=1,AD=3,CD=2.若点E是线段AD上的动点,则满足∠SEC=90°的点E的个数是( )| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | e1>e2 | B. | e1<e2 | C. | e1≤e2 | D. | e1≥e2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{x^2}{4}+\frac{y^2}{8}=1$ | B. | $\frac{x^2}{12}+\frac{y^2}{16}=1$ | C. | $\frac{x^2}{8}+\frac{y^2}{4}=1$ | D. | $\frac{x^2}{16}+\frac{y^2}{12}=1$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com