练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    17．几何体三视图如图所示，则几何体的体积为（　　）
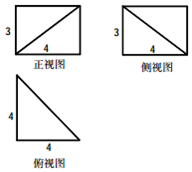
    A．32B．16C．8D．8$\sqrt{2}$

    分析 先由三视图判断出几何体的形状及度量长度，然后利用柱体和锥体体积公式，可计算答案．

    解答 解：由三视图得，该几何体为一个三棱柱切去一个同底同高的三棱锥所得的组合体，
    它们的底面面积S=$\frac{1}{2}$×4×4=8，
    高h=3，
    故组合体的体积V=Sh-$\frac{1}{3}$Sh=$\frac{2}{3}$Sh=16，
    故选：B．

    点评 解决三视图的题目，关键是由三视图判断出几何体的形状及度量长度，然后利用几何体的面积及体积公式解决．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    6．如图，在梯形ABCD中，AB∥CD，AD=DC=CB=2，∠ABC=60°，平面ACEF⊥平面ABCD，四边形ACEF是菱形，∠CAF=60°．
    （1）求证：BC⊥平面ACEF；
    （2）求平面ABF与平面ADF所成锐二面角的余弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    8．已知函数f（x）=|2x-1|-2|x-1|．
    （I）作出函数f（x）的图象；
    （Ⅱ）若不等式$\frac{a}{1-a}$≤f（x）有解，求实数a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    5．已知椭圆 C：$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1（ a＞b＞0）经过点 （1，$\frac{{\sqrt{3}}}{2}$），离心率为$\frac{{\sqrt{3}}}{2}$，点 A 为椭圆 C 的右顶点，直线 l 与椭圆相交于不同于点 A 的两个点P （x1，y1），Q （x2，y2）．
    （Ⅰ）求椭圆 C 的标准方程；
    （Ⅱ）当 $\overrightarrow{AP}$?$\overrightarrow{AQ}$=0 时，求△OPQ 面积的最大值；
    （Ⅲ）若直线 l 的斜率为 2，求证：△APQ 的外接圆恒过一个异于点 A 的定点．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

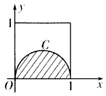    12．如图正方形的曲线C是以1为直径的半圆，从区间[0，1]上取1600个随机数x1，x2，…，x800，y1，y2，…，y800，已知800个点（x1，y1），（x2，y2），…，（x800，y800）落在阴影部分阴影部分的个数为m，则m的估计值为（　　）
    A．157B．314C．486D．628

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

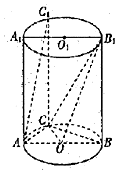    2．如图，在圆柱OO1中，矩形ABB1A1是过OO1的截面CC1是圆柱OO1的母线，AB=2，AA1=3，∠CAB=$\frac{π}{3}$．
    （1）证明：AC1∥平面COB1；
    （2）在圆O所在的平面上，点C关于直线AB的对称点为D，求二面角D-B1C-B的余弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    9．已知函数$f（x）=ln（{x+1}）-\frac{ax}{1-x}（{a∈R}）$．
    （1）当a=1时，求函数f（x）的单调区间；
    （2）若-1＜x＜1时，均有f（x）≤0成立，求实数a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    6．若命题“?x∈[-1，1]，1+2x+a•4x＜0”是假命题，则实数a的最小值为-6．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    7．在△ABC中，角A，B，C的对边分别为a，b，c，若c=2，a2=b2+1，则acosB=（　　）
    A．$\frac{5}{8}$B．$\frac{5}{4}$C．$\frac{5}{2}$D．5

    查看答案和解析>>

    同步练习册答案