
分析 先设x∈[-1,0],运用取相反数和奇函数的定义,转化为[0,1],利用周期性和符号把“x-4”转化到区间[-1,0],代入函数解析式,再利用周期性,求出f(x)在[3,4]上的解析式.
解答 解:设x∈[-1,0],则-x∈[0,1],
∵当x∈[0,1]时,f(x)=log2x,
∴f(-x)=log2(-x),
由f(x)为奇函数,即有f(-x)=-f(x),
则f(x)=-log2(-x),x∈[-1,0],
由函数y=f(x)是周期为4的函数,
令x∈[3,4],则x-4∈[-1,0],
即有f(x-4)=-log2(4-x),
则有f(x)=f(x-4)=-log2(4-x),x∈[3,4].
点评 本题考查了求定区间上的函数解析式,一般的做法是“求谁设谁”,即在那个区间上求解析式,x就设在该区间内,再利用函数的周期和负号转化到已知的区间上,代入解析式进行化简,再利用奇函数的定义和周期性求出f(x).


 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案科目:高中数学 来源: 题型:选择题
| A. | ($\frac{1}{2}$,+∞) | B. | [$\frac{1}{2}$,+∞) | C. | (-∞,$\frac{1}{2}$) | D. | (-∞,$\frac{1}{2}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
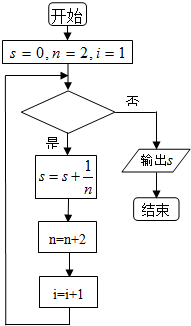
| A. | i≤11 | B. | i≤10 | C. | i≥10 | D. | i≥11 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (23,24) | B. | (24,27) | C. | (21,24) | D. | (24,25) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 既没有最大值也没有最小值 | B. | 有最大值5,没有最小值 | ||
| C. | 有最小值-1,没有最大值 | D. | 有最小值-5,也有最大值5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,2),3 | B. | (-1,2),9 | C. | (1,-2),3 | D. | (1,-2),9 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com