练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    13．已z0=2+2i，|z-z0|=$\sqrt{2}$，当z=1+i时，|z|有最小值，最小值为$\sqrt{2}$．

    分析 设出复数z，然后求出z的轨迹方程，利用复数的轨迹方程，结合几何意义求解即可．

    解答 解：设复数z=x+yi，z0=2+2i，|z-z0|=$\sqrt{2}$，
    则|z-z0|2=2，
    即（x-2）2+（y-2）2=2，
    复数z在复平面内对应的点的轨迹是以（2，2）为圆心以$\sqrt{2}$为半径的圆．
    可知|z|的最小值为：（$\sqrt{（0-2）^{2}+（0-2）^{2}}$-$\sqrt{2}$=$\sqrt{2}$，
    此时x=1，y=1，即z=1+i，
    故答案为：1+i，$\sqrt{2}$．

    点评 本题考查复数的代数形式的混合运算，复数的几何意义，复数的模的求法，考查计算能力．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    3．定义在R上的偶函数f（x）满足f（x）=f（x+2），当x∈[3，4]时，f（x）=x-2，则（　　）
    A．f（sin$\frac{1}{2}$）＜f（cos$\frac{1}{2}$）B．f（sin$\frac{π}{3}$）＞f（cos$\frac{π}{3}$）C．f（sin1）＜f（cos1）D．f（sin$\frac{π}{2}$）＞f（cos$\frac{π}{2}$）

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    4．求cos$\frac{7}{6}$π+sin$\frac{2}{3}$π-cos$\frac{8}{3}$π+sin$\frac{13}{6}$π+cos$\frac{17}{6}$π的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    1．已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的焦距为2，左、右顶点分别为A、B，P是椭圆上一点，记直线PA、PB的斜率为k1，k2，且k1k2=-$\frac{1}{2}$．
    （1）求椭圆C的方程；
    （2）若直线l：y=kx+m（k≠0）与椭圆C交于M、N两点，以M、N为直径的圆经过原点，且线段MN的垂直平分线在y轴上的截距为-$\frac{1}{5}$，求直线l的方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    8．已知A，B是锐角三角形的两个内角，则复数（sinA-cosB）+（sinB-cosA）i在复平面内对应的点位于（　　）
    A．第四象限B．第三象限C．第二象限D．第一象限

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

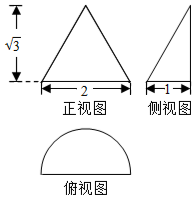    3．已知某几何体的三视图如图所示，则该几何体的表面积为（　　）
    A．$\frac{5π}{2}+\sqrt{3}$B．$\frac{3π}{2}+2$C．$\frac{π}{2}+\sqrt{3}$D．$\frac{3π}{2}+\sqrt{3}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    10．二项式${（{\frac{x}{{\sqrt{2}}}-y}）^8}$的展开式中，x4y4与x2y6项的系数之和是$\frac{63}{2}$（用数字作答）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    7．若i（bi+1）是纯虚数，i是虚数单位，则实数b=0．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    8．已知sin（π-α）=-2sin（$\frac{π}{2}$+α），则tanα的值为（　　）
    A．$\frac{1}{2}$B．2C．-$\frac{1}{2}$D．-2

    查看答案和解析>>

    同步练习册答案