
分析 写出二项式的通项公式,利用幂指数求解x4y4与x2y6项的系数之和.
解答 解:${(\frac{x}{{\sqrt{2}}}-y)^8}$的展开式的通项为${T_{r+1}}=C_8^r{(\frac{x}{{\sqrt{2}}})^{8-r}}{(-y)^r}=\frac{{{{(-1)}^r}}}{{{{(\sqrt{2})}^{8-r}}}}C_8^r{x^{8-r}}{y^r}$
当r=4时,可得x4y4的系数为$\frac{{{{(-1)}^4}}}{{{{(\sqrt{2})}^{8-4}}}}C_8^4=\frac{35}{2}$;
当r=6时,可得x2y6的系数为$\frac{{{{(-1)}^6}}}{{{{(\sqrt{2})}^{8-6}}}}C_8^6=14$;
所以x4y4与x2y6的系数之和是$\frac{35}{2}+14=\frac{63}{2}$.
故答案为:$\frac{63}{2}$.
点评 本题考查二项式定理的应用,系数的性质的求法,考查计算能力.


科目:高中数学 来源: 题型:解答题
 如图所示,在斜三棱柱ABC-A1B1C1中,AB=BC=1,AA1=2,D是AC的中点,AB⊥平面B1C1CB,∠BCC1=60°.
如图所示,在斜三棱柱ABC-A1B1C1中,AB=BC=1,AA1=2,D是AC的中点,AB⊥平面B1C1CB,∠BCC1=60°.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 10 | B. | 12 | C. | 14 | D. | 16 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
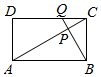 如图,在矩形ABCD中,AB=$\sqrt{3}$AD,点Q为线段CD(含端点)上一个动点,且$\overrightarrow{DQ}$=λ$\overrightarrow{QC}$,BQ交AC于P,且$\overrightarrow{AP}$=μ$\overrightarrow{PC}$,若AC⊥BP,则λ-μ=-1.
如图,在矩形ABCD中,AB=$\sqrt{3}$AD,点Q为线段CD(含端点)上一个动点,且$\overrightarrow{DQ}$=λ$\overrightarrow{QC}$,BQ交AC于P,且$\overrightarrow{AP}$=μ$\overrightarrow{PC}$,若AC⊥BP,则λ-μ=-1.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $C_{2016}^k{2^{2016-k}}{5^{k-1}}$ | B. | $C_{2016}^{k-1}{2^{2017-k}}{5^{k-1}}$ | ||
| C. | $C_{2016}^{k-1}$ | D. | $C_{2016}^k{2^{2016-k}}{5^k}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com