已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1的焦距为2.左.右顶点分别为A.B.P是椭圆上一点.记直线PA.PB的斜率为k1.k2.且k1k2=-$\frac{1}{2}$．(1)求椭圆C的方程,(2)若直线l:y=kx+m与椭圆C交于M.N两点.以M.N为直径的圆经过原点.且线段MN的垂直平分线在y轴上� 题目和参考答案——青夏教育精英家教网—

精英家教网 > 高中数学 > 题目详情

1．已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的焦距为2，左、右顶点分别为A、B，P是椭圆上一点，记直线PA、PB的斜率为k₁，k₂，且k₁k₂=-$\frac{1}{2}$．
（1）求椭圆C的方程；
（2）若直线l：y=kx+m（k≠0）与椭圆C交于M、N两点，以M、N为直径的圆经过原点，且线段MN的垂直平分线在y轴上的截距为-$\frac{1}{5}$，求直线l的方程．

分析（1）由题意可得c=1，设P（m，n），代入椭圆方程，运用直线的斜率公式，化简整理，计算可得a，b，进而得到椭圆方程；
（2）将直线l：y=kx+m（k≠0）代入椭圆x²+2y²-2=0，设M（x₁，y₁），N（x₂，y₂），运用韦达定理和中点坐标公式，以及两直线垂直的条件：斜率之积为-1，化简整理，解方程可得k，m，进而得到所求直线的方程．

解答解：（1）由题意可得c=1，即a²-b²=1，
设P（m，n），可得$\frac{{m}^{2}}{{a}^{2}}$+$\frac{{n}^{2}}{{b}^{2}}$=1，
即$\frac{{n}^{2}}{{m}^{2}-{a}^{2}}$=-$\frac{{b}^{2}}{{a}^{2}}$，
由题意可得A（-a，0），B（a，0），
即有k₁k₂=$\frac{n}{m+a}$•$\frac{n}{m-a}$=-$\frac{{b}^{2}}{{a}^{2}}$=-$\frac{1}{2}$，
解得a=$\sqrt{2}$，b=1，
可得椭圆的方程为$\frac{{x}^{2}}{2}$+y²=1；
（2）将直线l：y=kx+m（k≠0）代入椭圆x²+2y²-2=0，
可得（1+2k²）x²+4kmx+2m²-2=0，
判别式为16k²m²-8（1+2k²）（m²-1）＞0，
即有1+2k²＞m²，
设M（x₁，y₁），N（x₂，y₂），
可得x₁+x₂=-$\frac{4km}{1+2{k}^{2}}$，x₁x₂=$\frac{2{m}^{2}-2}{1+2{k}^{2}}$，
y₁y₂=（kx₁+m）（kx₂+m）=k²x₁x₂+km（x₁+x₂）+m²，
由题意OM⊥ON，可得x₁x₂+y₁y₂=0，
即为（1+k²）x₁x₂+km（x₁+x₂）+m²=0，
即（1+k²）•$\frac{2{m}^{2}-2}{1+2{k}^{2}}$+km（-$\frac{4km}{1+2{k}^{2}}$）+m²=0，
化简可得3m²=2+2k²，①
又MN的中点为（-$\frac{2km}{1+2{k}^{2}}$，$\frac{m}{1+2{k}^{2}}$），
由MN的垂直平分线经过点（0，-$\frac{1}{5}$），可得
垂直平分线的方程为y=-$\frac{1}{k}$x-$\frac{1}{5}$，
代入中点坐标可得$\frac{m}{1+2{k}^{2}}$=-$\frac{1}{k}$•（-$\frac{2km}{1+2{k}^{2}}$）-$\frac{1}{5}$，
化简可得5m=1+2k²，②
由①②解得m=$\frac{5+\sqrt{37}}{6}$（负的舍去），k=±$\frac{\sqrt{57+15\sqrt{37}}}{6}$，
检验判别式大于0成立，
直线l的方程为y=±$\frac{\sqrt{57+15\sqrt{37}}}{6}$x+$\frac{5+\sqrt{37}}{6}$．

点评本题考查椭圆的方程的求法，注意运用点满足椭圆方程以及直线的斜率公式，考查直线的方程的求法，注意联立直线和椭圆方程，运用韦达定理和中点坐标公式，以及直线垂直的条件，考查化简整理的运算能力，属于中档题．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：选择题

11．下列函数中，满足f（-x）+f（x）=0的单调递增函数是（　　）

A．

f（x）=x³

B．

f（x）=-x^-1

C．

f（x）=log₂x

D．

f（x）=2^x

查看答案和解析>>

科目：高中数学 来源： 题型：填空题

12．已知双曲线C的两条渐近线为l₁，l₂，过右焦点F作FB∥l₁且交l₂于点B，过点B作BA⊥l₂且交l₁于点A，若AF⊥x轴，则双曲线C的离心率为$\frac{2\sqrt{3}}{3}$．

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

9．

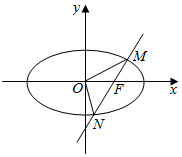如图：已知椭圆E：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0），过右焦点F（1，0）的直线l与椭圆E交于M、N两点，且满足$\overrightarrow{MF}$=$\frac{1}{2}$$\overrightarrow{FN}$．
（1）当直线l的倾斜角为45°时，求椭圆E的方程；
（2）求△OMN面积的最大值及此时椭圆E的离心率e．

查看答案和解析>>

科目：高中数学 来源： 题型：选择题

16．已知x，y满足$\left\{\begin{array}{l}{x+2y≤4}\\{x-y≤1}\\{x+2≥0}\end{array}\right.$，目标函数z=1-2x-y的最大值为a，最小值为b，则a-b=（　　）

A．

B．

C．

D．

查看答案和解析>>

科目：高中数学 来源： 题型：选择题

6．如果0＜a＜1＜b，c=log_ab+log_ba+2（　　）

A．

c＞0