Question

已知点P是抛物线y²=-8x上一点，设P到此抛物线准线的距离是d₁，到直线x+y-10=0的距离是d₂，则d₁+d₂的最小值是

 

．

Answer 1

考点：抛物线的简单性质

专题：综合题,圆锥曲线的定义、性质与方程

分析：根据抛物线的方程，得到焦点为F（-2，0），准线方程是x=2．然后作PQ与垂直准线，交于点Q，过作PM与直线x+y-10=0垂直，交于点M，可得PQ=d₁，PM=d₂．连接PF，根据抛物线的定义可得d₁+d₂=PF+PM，因此当P、F、M三点共线且与直线x+y-10=0垂直时，d_l+d₂最小，最后用点到直线的距离公式，可求出这个最小值．

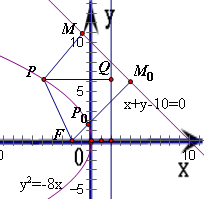
解答： 解：∵抛物线方程是y²=-8x，
∴抛物线的焦点为F（-2，0），准线方程是x=2
P是抛物线y²=-8x上一点，过P点作PQ与准线垂直，垂足为Q，
再过P作PM与直线x+y-10=0垂直，垂足为M
则PQ=d₁，PM=d₂
连接PF，根据抛物线的定义可得PF=PQ=d₁，所以d₁+d₂=PF+PM，
可得当P、F、M三点共线且与直线x+y-10=0垂直时，d_l+d₂最小．（即图中的F、P₀、M₀位置）
∴d_l+d₂的最小值是焦点F到直线x+y-10=0的距离，
即（d_l+d₂）_min=

|-2+0-10|

1+1

=6

2

．
故答案为：6

2

．

点评：本题借助于求抛物线上一动点到两条定直线的距离之和的最小值问题，考查了抛物线的定义与简单几何性质和点到直线距离公式等知识点，属于中档题．