
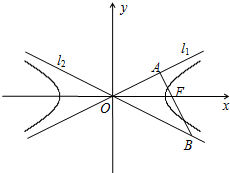
 如图,双曲线的中心为原点O,焦点在x轴上,两条渐近线分别为l1,l2,经过右焦点F垂直于l1的直线分别交l1,l2于A,B两点.且|OA|+|OB|=2|AB|.
如图,双曲线的中心为原点O,焦点在x轴上,两条渐近线分别为l1,l2,经过右焦点F垂直于l1的直线分别交l1,l2于A,B两点.且|OA|+|OB|=2|AB|.分析 (1)利用极限方程,通过|OA|+|OB|=2|AB|转化求出$|{OA}|=\frac{3}{5}|{OB}|$,推出$2{(\frac{a}{c})^2}-1=\frac{3}{5}$,解得离心率.
(2)通过$e=\frac{{\sqrt{5}}}{2}$,可设a=2t(t>0),双曲线方程表示为$\frac{x^2}{{4{t^2}}}-\frac{y^2}{t^2}=1$;联立直线AB方程与双曲线方程,利用弦长公式求解即可.
解答 解:(1)由题意,得F(c,0),l1的方程为bx-ay=0,∴$|{FA}|=\frac{bc}{{\sqrt{{b^2}+{{(-a)}^2}}}}=b$,从而|OA|=a;
由|OA|+|OB|=2|AB|得:$|{AB}|=\frac{1}{2}(|{OA}|+|{OB}|)$,联立|OA|2+|AB|2=|OB|2,得5|OA|2+2|OA|•|OB|-3|OB|2=0,解得$|{OA}|=\frac{3}{5}|{OB}|$,所以$cos∠AOB=\frac{{|{OA}|}}{{|{OB}|}}=\frac{3}{5}$
∵cos∠AOB=cos2∠AOF=2cos2∠AOF-1,∴$2{(\frac{a}{c})^2}-1=\frac{3}{5}$,解得离心率$e=\frac{c}{a}=\frac{{\sqrt{5}}}{2}$…(6分)
(2)由(1)$e=\frac{{\sqrt{5}}}{2}$,可设a=2t(t>0),则$c=\sqrt{5}t$,从而b=t,因此双曲线方程$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$可表示为$\frac{x^2}{{4{t^2}}}-\frac{y^2}{t^2}=1$;过F的直线AB方程为$y=-2(x-\sqrt{5}t)$,联立$\left\{\begin{array}{l}\frac{x^2}{{4{t^2}}}-\frac{y^2}{t^2}=1\\ y=-2(x-\sqrt{5}t)\end{array}\right.$,整理得:$15{x^2}-32\sqrt{5}tx+84{t^2}=0$,由韦达定理得:${x_1}+{x_2}=\frac{{32\sqrt{5}}}{15}t$,${x_1}•{x_2}=\frac{28}{5}{t^2}$,由题设得$4=\sqrt{[{1+{{(-2)}^2}}][{{{({x_1}+{x_2})}^2}-4{x_1}{x_2}}]}=\frac{4}{3}t$,解得t=3,故所求的双曲线方程为$\frac{x^2}{36}-\frac{y^2}{9}=1$.…(12分)
点评 本题考查双曲线方程的求法,双曲线的离心率以及弦长公式的求法,考查计算能力以及转化思想的应用.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{{\sqrt{3}}}{2}$ | B. | $\frac{{\sqrt{3}}}{2}$ | C. | $-\frac{1}{2}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,1] | B. | [-1,1] | C. | {0,1} | D. | {-1,0,1} |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {3,7,9} | B. | {1,5} | C. | {2,6,8} | D. | {4} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{{\sqrt{3}}}{6}$ | B. | $\frac{{\sqrt{3}}}{6}$ | C. | $-\frac{{\sqrt{3}}}{3}$ | D. | $\frac{{\sqrt{3}}}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com