
分析 ①根据正方体中取对应的对角线构成的四面体是正四面体.
②底面是等边三角形,侧面都是等腰三角形的三棱锥不一定是正三棱锥;
③当有两个侧面垂直于底面时,该四棱柱不一定为直四棱柱;
④一个棱锥不能有两条侧棱和底面垂直;
⑤一个棱锥可以有两个侧面和底面垂直;
⑥所有侧面都是正方形的四棱柱不一定是正方体.
解答 解:①在正方体上任意选择4个不共面的顶点,它们可能是正四面体的4个顶点正确,如图四面体B1-ACD1是正四面体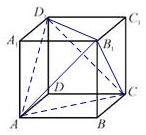 ;
;
②底面是等边三角形,侧面都是等腰三角形的三棱锥不一定是正三棱锥,
如图所示,
若AB=BC=AC=VA,且VA⊥平面ABC,但三棱锥V-ABC表示正三棱锥,∴②错误;
③当有两个侧面垂直于底面时,该四棱柱不一定为直四棱柱,
如两个侧面不是相邻的时,侧棱与底面不一定垂直,∴③错误;
④一个棱锥不能有两条侧棱和底面垂直,否则,这两条侧棱互相平行,∴④错误;
⑤一个棱锥可以有两个侧面和底面垂直,如②中图形,∴⑤正确;
⑥所有侧面都是正方形的四棱柱不一定是正方体,
∵各相邻侧面并不一定都互相垂直,∴⑥错误.
故答案为:①⑤
点评 本题主要考查空间中的柱、锥、体的结构特征的应用问题,解题时应对每一个命题进行分析判断,是综合题目.


 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案科目:高中数学 来源: 题型:选择题
| A. | (-∞,-3) | B. | (-∞,-3] | C. | (-3,+∞) | D. | [-3,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | p∧q | B. | ¬p∧¬q | C. | p∧¬q | D. | ¬p∧q |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,三棱锥P-ABC中,PA⊥平面ABC,AB⊥BC,D为PC的中点,E为PB的中点.
如图,三棱锥P-ABC中,PA⊥平面ABC,AB⊥BC,D为PC的中点,E为PB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{3}{4}$ | B. | -$\frac{4}{3}$ | C. | $\frac{3}{4}$ | D. | $\frac{4}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (x+$\frac{1}{x}$)′=1+$\frac{1}{{x}^{2}}$ | B. | (3x)′=3x•log3e | C. | (log2x)′=$\frac{1}{xln2}$ | D. | (x2cosx)′=-2sinx |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 3 | C. | $\frac{9}{2}$ | D. | $\frac{11}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
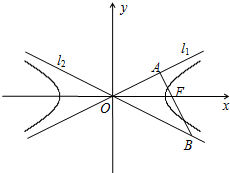 如图,双曲线的中心为原点O,焦点在x轴上,两条渐近线分别为l1,l2,经过右焦点F垂直于l1的直线分别交l1,l2于A,B两点.且|OA|+|OB|=2|AB|.
如图,双曲线的中心为原点O,焦点在x轴上,两条渐近线分别为l1,l2,经过右焦点F垂直于l1的直线分别交l1,l2于A,B两点.且|OA|+|OB|=2|AB|.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com