
| A. | $-\frac{{\sqrt{3}}}{6}$ | B. | $\frac{{\sqrt{3}}}{6}$ | C. | $-\frac{{\sqrt{3}}}{3}$ | D. | $\frac{{\sqrt{3}}}{3}$ |
分析 把|$\overrightarrow{a}$+$\overrightarrow{b}$|=$\sqrt{5}$两边平方,代入数量积公式即可求得向量$\overrightarrow{a}$与$\overrightarrow{b}$夹角的余弦值.
解答 解:由|$\overrightarrow{a}$|=$\sqrt{3}$,|$\overrightarrow{b}$|=2,|$\overrightarrow{a}$+$\overrightarrow{b}$|=$\sqrt{5}$,
得${(\overrightarrow{a}+\overrightarrow{b})}^{2}$=5,
即${|\overrightarrow{a}|}^{2}$+2$\overrightarrow{a}$•$\overrightarrow{b}$+${|\overrightarrow{b}|}^{2}$=5,
所以3+2×$\sqrt{3}$×2cos<$\overrightarrow{a}$,$\overrightarrow{b}$>+4=5,
解得cos<$\overrightarrow{a}$,$\overrightarrow{b}$>=-$\frac{\sqrt{3}}{6}$;
即向量$\overrightarrow a$与$\overrightarrow b$夹角的余弦值为-$\frac{\sqrt{3}}{6}$.
故选:A.
点评 本题考查了平面向量数量积与模长、夹角公式的应用问题,是基础题目.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
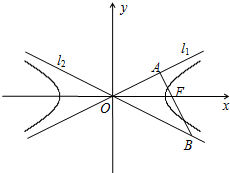 如图,双曲线的中心为原点O,焦点在x轴上,两条渐近线分别为l1,l2,经过右焦点F垂直于l1的直线分别交l1,l2于A,B两点.且|OA|+|OB|=2|AB|.
如图,双曲线的中心为原点O,焦点在x轴上,两条渐近线分别为l1,l2,经过右焦点F垂直于l1的直线分别交l1,l2于A,B两点.且|OA|+|OB|=2|AB|.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (2,+∞) | B. | (0,2) | C. | [0,2) | D. | [2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{5π}{6}$ | D. | $\frac{3π}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com