
分析 (Ⅰ)把曲线C1的参数方程变形,然后两边平方作和即可得到普通方程,可知曲线C1是圆,化为一般式,结合x2+y2=ρ2,y=ρsinθ化为极坐标方程;
(Ⅱ)化曲线C2、C3的极坐标方程为直角坐标方程,由条件可知y=x为圆C1与C2的公共弦所在直线方程,把C1与C2的方程作差,结合公共弦所在直线方程为y=2x可得1-a2=0,则a值可求.
解答 解:(Ⅰ)由$\left\{\begin{array}{l}x=acost\\ y=1+asint\end{array}\right.$,得$\left\{\begin{array}{l}{x=acost}\\{y-1=asint}\end{array}\right.$,两式平方相加得,x2+(y-1)2=a2.
∴C1为以(0,1)为圆心,以a为半径的圆.
化为一般式:x2+y2-2y+1-a2=0.①
由x2+y2=ρ2,y=ρsinθ,得ρ2-2ρsinθ+1-a2=0;
(Ⅱ)C2:ρ=4cosθ,两边同时乘ρ得ρ2=4ρcosθ,
∴x2+y2=4x,②
即(x-2)2+y2=4.
由C3:θ=α0,其中α0满足tanα0=2,得y=2x,
∵曲线C1与C2的公共点都在C3上,
∴y=2x为圆C1与C2的公共弦所在直线方程,
①-②得:4x-2y+1-a2=0,即为C3 ,
∴1-a2=0,
∴a=1(a>0).
点评 本题考查参数方程即简单曲线的极坐标方程,考查了极坐标与直角坐标的互化,训练了两圆公共弦所在直线方程的求法,是基础题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
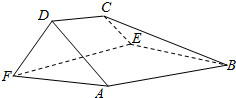 如图,在以A,B,C,D,E,F为顶点的五面体中,面ABEF为正方形,AF=2FD,∠AFD=90°,且二面角D-AF-E与二面角C-BE-F都是60°.
如图,在以A,B,C,D,E,F为顶点的五面体中,面ABEF为正方形,AF=2FD,∠AFD=90°,且二面角D-AF-E与二面角C-BE-F都是60°.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 上年度出险次数 | 0 | 1 | 2 | 3 | 4 | ≥5 |
| 保费 | 0.85a | a | 1.25a | 1.5a | 1.75a | 2a |
| 出险次数 | 0 | 1 | 2 | 3 | 4 | ≥5 |
| 频数 | 60 | 50 | 30 | 30 | 20 | 10 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com