
分析 (1)求出函数的导数,解关于导函数的方程,求出函数的单调区间,从而求出函数的极值即可;
(2)求出x1-x2<$\frac{1}{a}$(1-ln$\frac{1}{a}$),得到$\frac{{x}_{1}}{{x}_{2}}$=$\frac{{e}^{{ax}_{1}}}{{e}^{{ax}_{2}}}$=eax1-ax2,代入整理即可.
解答 解:(1)f(x)=x-eax(a>0),则f′(x)=1-aeax,
令f′(x)=1-aeax=0,则x=$\frac{1}{a}$ln $\frac{1}{a}$.
当x变化时,f′(x),f(x)的变化情况如下表:
| x | (-∞,$\frac{1}{a}$ln$\frac{1}{a}$) | $\frac{1}{a}$ln $\frac{1}{a}$ | ($\frac{1}{a}$ln$\frac{1}{a}$,+∞) |
| f′(x) | + | 0 | - |
| f(x) | ↗ | $\frac{1}{a}$ln $\frac{1}{a}$-$\frac{1}{a}$ | ↘ |
点评 本题考查了函数的单调性、极值问题,考查导数的应用以及不等式的证明,是一道中档题.


科目:高中数学 来源: 题型:选择题
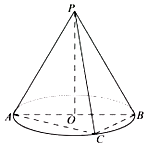 如图,设AB为圆锥PO的底面直径,PA为母线,点C在底面圆周上,若PA=AB=2,AC=BC,则二面角P-AC-B大小的正切值是( )
如图,设AB为圆锥PO的底面直径,PA为母线,点C在底面圆周上,若PA=AB=2,AC=BC,则二面角P-AC-B大小的正切值是( )| A. | $\frac{{\sqrt{6}}}{6}$ | B. | $\sqrt{6}$ | C. | $\frac{{\sqrt{7}}}{7}$ | D. | $\sqrt{7}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $arcsin(-\frac{3}{5})$ | B. | $π+arcsin\frac{3}{5}$ | C. | $2π-arcsin\frac{3}{5}$ | D. | $π-arcsin\frac{3}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 男 | 女 | 总计 | |
| 喜欢吃零食 | 5 | 12 | 17 |
| 不喜欢吃零食 | 40 | 28 | 68 |
| 总计 | 45 | 40 | 85 |
| P(K2≥k) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com