练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    13．已知复数z=2+i，则z4-4z3+6z2-4z-1=-6．

    分析 可将条件转化为（z-2）2=i2=-1，即z2-4z+4=-1，代入代数式整理即可，法二：观察知，原式=（z-1）4-2，将z=2+i代入化简即可．

    解答 解：∵z=2+i，
    ∴（z-2）2=i2=-1，
    ∴z4-4z3+6z2-4z-1
    =z4-4z3+5z2-5+（z-2）2
    =z4-4z3+4z2+z2-6
    =z2（z-2）2+z2-6
    =-6，
    另：观察知，
    原式=（z-1）4-2=（2+i-1）4-2=（1+i）4-2=（2i）2-2=-6；
    故答案为：-6．

    点评 本题考查复数代数形式的混合运算，结合题意转化条件，也是简化解题观察的根本，仔细分析题意，确定解题方向比直接上手解答好得多．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    3．已知复数$\frac{2a+i}{1+i}$是纯虚数，则实数a=（　　）
    A．-1B．$\frac{1}{2}$C．lD．-$\frac{1}{2}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    4．已知函数f（x）=x-eax（a＞0）（e是自然对数的底数），
    （1）求函数y=f（x）的极值；
    （2）若存在x1，x2（x1＜x2），使得f（x1）=f（x2）=0，证明：$\frac{x_1}{x_2}＜ae$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    1．已知$|{\overrightarrow a}|=|{\overrightarrow b}|=|{\overrightarrow c}$|=1，且$\overrightarrow a+\overrightarrow b+\sqrt{3}$$\overrightarrow c=0$，则$\overrightarrow a\overrightarrow b+\overrightarrow b\overrightarrow c+\overrightarrow c\overrightarrow a$=$\frac{1}{2}$-$\sqrt{3}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    8．设a∈R，函数$f（x）=\frac{1}{3}{x^3}-\frac{1}{2}（2a+1）{x^2}+bx+d$的图象如图．
    （1）已知f′（x）是f（x）的导函数，且$g（x）=\frac{f'（x）}{x}（x≠0）$为奇函数，求a的值；
    （2）若函数f（x）在x=2处取得极小值，求函数f（x）的单调递增区间．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    18．求值sin17°cos47°-sin73°cos43°=-$\frac{1}{2}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    5．已知椭圆$\frac{x^2}{4}+\frac{y^2}{16}$=1与$\frac{x^2}{4+n}+\frac{y^2}{16+n}$=1（n＞0），则下述结论中正确的是（　　）
    A．有相等的长轴长B．有相等的焦距C．有相等的离心率D．有相同的顶点

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    2．在直角坐标系xOy中，以O为极点，x轴正半轴为极轴建立极坐标系，圆C1，直线C2的极坐标方程分别为ρ=4sinθ，ρcos（θ-$\frac{π}{4}$）=2$\sqrt{2}$．求C1与C2交点的极坐标；（ρ＜0，0≤θ＜2π）

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

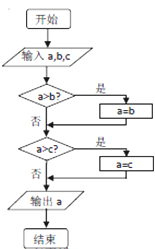
    3．执行如图的程序框图，若输入的a=π-1，b=ln$\frac{1}{3}$，c=20.1，则输出的结果a为（　　）
    A．20.1B．ln$\frac{1}{3}$C．π-1D．无法确定

    查看答案和解析>>

    同步练习册答案