
分析 由条件求得$\overrightarrow{a}•\overrightarrow{b}$=$\frac{1}{2}$ 且 $\overrightarrow{a}+\overrightarrow{b}$=-$\sqrt{3}$$\overrightarrow{c}$,代入要求的式子化简可得结果.
解答 解:已知$|{\overrightarrow a}|=|{\overrightarrow b}|=|{\overrightarrow c}$|=1,且$\overrightarrow a+\overrightarrow b+\sqrt{3}$$\overrightarrow c=0$,∴${\overrightarrow{a}}^{2}$+${\overrightarrow{b}}^{2}$+2$\overrightarrow{a}•\overrightarrow{b}$=3${\overrightarrow{c}}^{2}$,即 2+2$\overrightarrow{a}•\overrightarrow{b}$=3,∴$\overrightarrow{a}•\overrightarrow{b}$=$\frac{1}{2}$.
又 $\overrightarrow{a}+\overrightarrow{b}$=-$\sqrt{3}$$\overrightarrow{c}$,∴$\overrightarrow a\overrightarrow b+\overrightarrow b\overrightarrow c+\overrightarrow c\overrightarrow a$=$\overrightarrow{a}•\overrightarrow{b}$+$\overrightarrow{c}$•($\overrightarrow{a}$+$\overrightarrow{b}$)=$\overrightarrow{a}•\overrightarrow{b}$+$\overrightarrow{c}$•(-$\sqrt{3}$$\overrightarrow{c}$)=$\frac{1}{2}$-$\sqrt{3}$,
故答案为:$\frac{1}{2}$-$\sqrt{3}$.
点评 本题主要考查两个向量的数量积的运算,属于基础题.


 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 男 | 女 | 总计 | |
| 喜欢吃零食 | 5 | 12 | 17 |
| 不喜欢吃零食 | 40 | 28 | 68 |
| 总计 | 45 | 40 | 85 |
| P(K2≥k) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
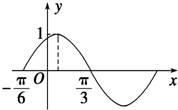 函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,若x1,x2∈(-$\frac{π}{6}$,$\frac{π}{3}$),且f(x1)=f(x2),则f(x1+x2)=$\frac{\sqrt{3}}{2}$.
函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,若x1,x2∈(-$\frac{π}{6}$,$\frac{π}{3}$),且f(x1)=f(x2),则f(x1+x2)=$\frac{\sqrt{3}}{2}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com