
分析 由于不等式ax2+bx+c≤0的解集为$\left\{{x|x≤-\frac{1}{3}或x≥2}\right\}$,可得:$-\frac{1}{3}$,2 是一元二次方程ax2+bx+c=0的两个实数根,利用根与系数的关系可把不等式cx2+bx+a>0化为二次不等式即可解出.
解答 解:由题意可知,a<0且方程ax2+bx+c=0的两根为$-\frac{1}{3}$,2 …(3分)
∴$-\frac{b}{a}=\frac{5}{3}$,$\frac{c}{a}=-\frac{2}{3}$,
∴$b=-\frac{5}{3}a$,$c=-\frac{2}{3}a$…(6分)
∴不等式cx2+bx+a>0,
即$-\frac{2}{3}a{x^2}-\frac{5}{3}ax+a>0$,
∴2x2+5x-3>0…(9分),
∴(2x-1)(x+3)>0,
解得$x<-3或x>\frac{1}{2}$…(11分),
∴不等式cx2+bx+a>0的解集为$\left\{{x|x<-3或x>\frac{1}{2}}\right\}$.…(12分)
点评 本题考查了一元二次不等式的解法、一元二次方程的根与系数的关系,考查了推理能力和计算能力,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\sqrt{2}$ | C. | 4 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
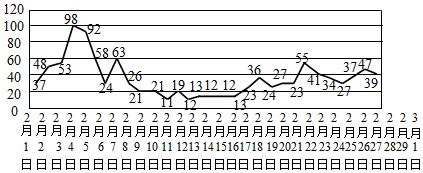
| 空气质量指数类别 | 频数 | 频率 |
| 优[0,35] | ||
| 良(35,75] | ||
| 轻度污染(75,115] | ||
| 中度污染(115,150] | ||
| 重度污染(150,250] | ||
| 严重污染(250,500] | ||
| 合计 | 30 | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,1) | B. | ($\frac{1}{2}$,1) | C. | ($\frac{\sqrt{2}}{2}$,1) | D. | [$\frac{\sqrt{2}}{2}$,1) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com