
分析 利用向量垂直的条件,结合向量数量积公式,即可求向量$\overrightarrow{a}$和$\overrightarrow{b}$的夹角,从而求出$|{2\overrightarrow a-\overrightarrow b}|$的值.
解答 解:设向量$\overrightarrow{b}$和$\overrightarrow{a}$的夹角是α,则
∵|$\overrightarrow{a}$|=$\sqrt{2}$,|$\overrightarrow{b}$|=2,且($\overrightarrow{a}$-$\overrightarrow{b}$)⊥$\overrightarrow{a}$,
∴($\overrightarrow{a}$-$\overrightarrow{b}$)•$\overrightarrow{a}$=2-$\overrightarrow{a}$•$\overrightarrow{b}$=2-2$\sqrt{2}$cosα
∴cosα=$\frac{\sqrt{2}}{2}$,
∴${(|2\overrightarrow{a}-\overrightarrow{b}|)}^{2}$=4${\overrightarrow{a}}^{2}$+${\overrightarrow{b}}^{2}$-4$\overrightarrow{a}$•$\overrightarrow{b}$=8+4-4×$\sqrt{2}$×2×$\frac{\sqrt{2}}{2}$=4
故$|{2\overrightarrow a-\overrightarrow b}|$=2,
故答案为:2.
点评 本题考查向量的夹角的计算,考查向量数量积公式的运用,属于基础题.


科目:高中数学 来源:2016-2017学年新疆库尔勒市高二上学期分班考试数学(理)试卷(解析版) 题型:解答题
在锐角△ABC中,a、b、c分别为角A、B、C所对的边,且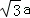 =2csinA
=2csinA
(1)确定角C的大小;
(2)若c=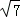 ,且△ABC的面积为
,且△ABC的面积为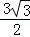 ,求a+b的值
,求a+b的值
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x+y+1=0 | B. | 2x+y+5=0 | C. | 2x+3y+1=0 | D. | x+3y-5=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|x>-2} | B. | {x|0<x<1} | C. | {x|x<1} | D. | {x|-2<x<1} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{10}{9}$ | B. | $\frac{14}{9}$ | C. | $\frac{5}{3}$ | D. | $\frac{3}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,0) | B. | (-∞,-1) | C. | (-1,+∞) | D. | (0,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
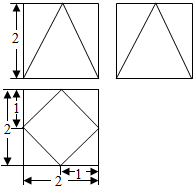 一个正方体截去四个角得到一个多面体,其三视图如图所示,则该多面体的体积为( )
一个正方体截去四个角得到一个多面体,其三视图如图所示,则该多面体的体积为( )| A. | 4 | B. | $\frac{20}{3}$ | C. | $\frac{4}{3}$(3+$\sqrt{2}$) | D. | $\frac{16}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com