
(本小题满分12分)从广州某高校男生中随机抽取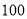 名学生,测得他们的身高(单位: cm)情况如表1:
名学生,测得他们的身高(单位: cm)情况如表1:
分组 | 频数 | 频率 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
合计 |
|
|
表1
(1)求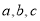 的值;
的值;
(2)按表1的身高组别进行分层抽样, 从这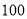 名学生中抽取
名学生中抽取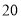 名担任广州国际马拉松志愿者, 再从身高不低于
名担任广州国际马拉松志愿者, 再从身高不低于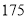 cm的志愿者中随机选出
cm的志愿者中随机选出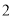 名担任迎宾工作, 求这
名担任迎宾工作, 求这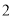 名担任迎宾工作的志愿者中至少有
名担任迎宾工作的志愿者中至少有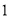 名的身高不低于
名的身高不低于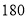 cm的概率.
cm的概率.
(1)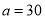 ,
,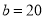 ,
,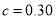 ;(2)
;(2)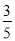 .
.
【解析】
试题分析:(1)先利用频率之和为1求出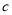 的值,再利用
的值,再利用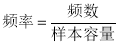 求出
求出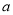 的值,进而利用频数之和为100求出
的值,进而利用频数之和为100求出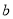 的值;(2)利用列举法写出从身高不低于
的值;(2)利用列举法写出从身高不低于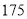 cm的志愿者中随机选出
cm的志愿者中随机选出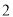 名担任迎宾工作的所有基本事件,并从中找出这
名担任迎宾工作的所有基本事件,并从中找出这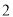 名担任迎宾工作的志愿者中至少有
名担任迎宾工作的志愿者中至少有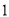 名的身高不低于
名的身高不低于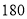 cm的基本事件,利用古典概型公式求出概率.
cm的基本事件,利用古典概型公式求出概率.
试题解析:(1)【解析】
由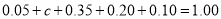 ,得
,得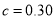 . 1分
. 1分
由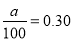 ,得
,得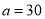 , 2分
, 2分
由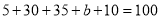 ,得
,得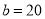 . 3分
. 3分
(2)【解析】
依据分层抽样的方法,抽取的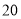 名志愿者中身高在区间
名志愿者中身高在区间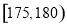 上的有
上的有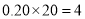 名,记为
名,记为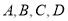 ; 5分
; 5分
而身高在区间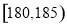 上的有
上的有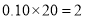 名,记为
名,记为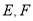 . 7分
. 7分
记“这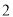 名担任迎宾工作的志愿者中至少有
名担任迎宾工作的志愿者中至少有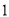 名的身高不低于
名的身高不低于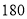 cm”为事件
cm”为事件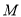 ,
,
从身高不低于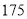 cm的志愿者中随机选出
cm的志愿者中随机选出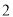 名担任迎宾工作,共有
名担任迎宾工作,共有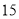 种不同取法:
种不同取法: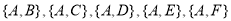 ,
,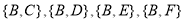 ,
,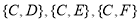 ,
,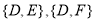 ,
,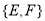 . 9分
. 9分
事件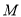 包含的基本事件有
包含的基本事件有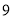 种:
种: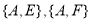 ,
,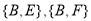 ,
,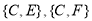 ,
,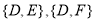 ,
,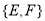 . 11分
. 11分
∴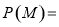
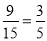 为所求. 12分
为所求. 12分
考点:1、频率分布表;2、古典概型;3、分层抽样.
考点分析: 考点1:古典概率 试题属性

科目:高中数学 来源:2014-2015学年江西省吉安市高三上学期第二次阶段考试理科数学试卷(解析版) 题型:解答题
已知函数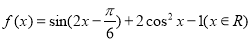 .
.
(1)求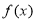 的单调递增区间;
的单调递增区间;
(2)在△ABC中,三内角A,B,C的对边分别为a,b,c,已知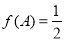 ,b,a,c成等差数列,且
,b,a,c成等差数列,且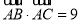 ,求a的值.
,求a的值.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年广东省广州市毕业班综合测试一文科数学试卷(解析版) 题型:选择题
设抛物线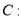
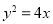 上一点
上一点 到
到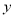 轴的距离为
轴的距离为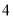 ,则点
,则点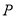 到抛物线
到抛物线 的焦点的距离是( )
的焦点的距离是( )
A.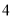 B.
B.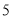 C.
C.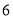 D.
D.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年吉林省长春市高三上学期阶段性考试文科数学试卷(解析版) 题型:选择题
已知双曲线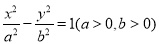 的一个焦点到一条渐近线的距离为
的一个焦点到一条渐近线的距离为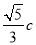 (
(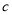 为双曲线的半焦距长),则该双曲线的离心率为( )
为双曲线的半焦距长),则该双曲线的离心率为( )
A.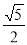 B.
B.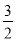 C.
C.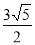 D.
D.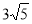
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com