
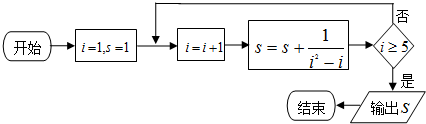
| A. | $\frac{4}{5}$ | B. | $\frac{9}{5}$ | C. | $\frac{5}{6}$ | D. | $\frac{11}{6}$ |
 步步高达标卷系列答案
步步高达标卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 十一长假期间,各旅游景点游客爆满,甚至发生了游客滞留事件,某著名风景点的工作人员总结了前几年的经验,提前为部分游客设计了旅游路线图,其中的一条平面观光路线DEFD,如图所示
十一长假期间,各旅游景点游客爆满,甚至发生了游客滞留事件,某著名风景点的工作人员总结了前几年的经验,提前为部分游客设计了旅游路线图,其中的一条平面观光路线DEFD,如图所示查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|x≤0} | B. | {x|1≤x≤2} | C. | {x|0≤x<1或x>2} | D. | {x|0≤x<1或x≥2} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com