
 如图,DC⊥平面ABC,EB∥DC,AC=BC=EB=2DC=2,∠ACB=120°,Q为AB的中点
如图,DC⊥平面ABC,EB∥DC,AC=BC=EB=2DC=2,∠ACB=120°,Q为AB的中点分析 (Ⅰ)推导出BE⊥平面ABC,从而CQ⊥BE,再求出CQ⊥AB,由此能证明CQ⊥平面ABE.
(Ⅱ)过点A作AM⊥BC,交BC延长线于点M,推导出AM⊥平面BEDC,从而${V}_{A-CED}=\frac{1}{3}{S}_{△CDE}•AM$,由此能求出多面体ACED的体积.
(Ⅲ)延长EO,交BC延长线于S,过点M作MQ⊥ES于Q,连结AQ,则∠AQM为A-DE-B的平面角,由此能求出二面角A-DE-B的正切值.
解答 证明:(Ⅰ)∵DC⊥平面ABC,BE∥DC,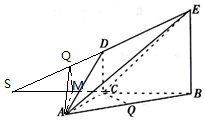
∴BE⊥平面ABC,
∴CQ⊥BE,
又∵AC=BC=2,点Q为AB边中点,
∴CQ⊥AB,
∵AB∩BE=B,∴CQ⊥平面ABE.
(Ⅱ)过点A作AM⊥BC,交BC延长线于点M,
∵AM⊥BC,AM⊥BE,
∴AM⊥平面BEDC,
∴${V}_{A-CED}=\frac{1}{3}{S}_{△CDE}•AM$,
∴AM=$AC•sin\frac{π}{3}$=$\sqrt{3}$,${S}_{△CDE}=\frac{1}{2}×1×2=1$,
∴多面体ACED的体积${V}_{A-CED}=\frac{1}{3}×1×\sqrt{3}$=$\frac{\sqrt{3}}{3}$.
(Ⅲ)延长EO,交BC延长线于S,
过点M作MQ⊥ES于Q,连结AQ,
由(Ⅱ)得∠AQM为A-DE-B的平面角,
∵CD$\underset{∥}{=}$$\frac{1}{2}$BC,∴SC=CB=2,
∴SE=$\sqrt{B{E}^{2}+S{B}^{2}}$=$2\sqrt{5}$,
MC=MS=1,
△SQM∽△SBE,∴$\frac{QM}{BE}=\frac{SM}{SE}$,
∴$\frac{QM}{2}=\frac{1}{2\sqrt{5}}$,∴QM=$\frac{\sqrt{5}}{5}$,
∴∠AQM=$\frac{AM}{QM}=\frac{\sqrt{3}}{\frac{\sqrt{5}}{5}}$=$\sqrt{15}$.
∴二面角A-DE-B的正切值为$\sqrt{15}$.
点评 本题考查线面垂直的证明,考查多面体的体积的求法,考查二面角的正切值的求法,考查推理论证能力、运算求解能力,考查化归与转化思想、函数与方程思想,是中档题.


 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{5}}{5}$ | B. | $\frac{2\sqrt{5}}{5}$ | C. | $\frac{1}{5}$ | D. | $\frac{2}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 运行程序,输入n=4,则输出y的值是( )
运行程序,输入n=4,则输出y的值是( )| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}-\sqrt{6}}{4}$ | C. | $\frac{\sqrt{6}+\sqrt{2}}{4}$ | D. | $\frac{\sqrt{6}-\sqrt{2}}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图,△AOB为等腰直角三角形,OA=l,OC为斜边AB的髙,点P在射线OC 上,则$\overrightarrow{AP}$•$\overrightarrow{OP}$的最小值为( )
如图,△AOB为等腰直角三角形,OA=l,OC为斜边AB的髙,点P在射线OC 上,则$\overrightarrow{AP}$•$\overrightarrow{OP}$的最小值为( )| A. | -1 | B. | -$\frac{1}{4}$ | C. | -$\frac{1}{8}$ | D. | 0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
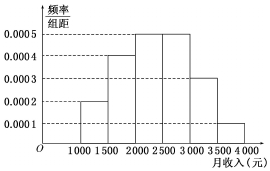 某市统计局就本地居民的月收入调查了10000人,并根据所得数据画了样本的频率分布直方图(每个分组包括左端点,不包括右端点,如第一组表示月收入在[1000,1500)(单位:元)).
某市统计局就本地居民的月收入调查了10000人,并根据所得数据画了样本的频率分布直方图(每个分组包括左端点,不包括右端点,如第一组表示月收入在[1000,1500)(单位:元)).查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com