
【题目】设数列![]() 是公比大于
是公比大于![]() 的等比数列,
的等比数列,![]() 是其前
是其前![]() 项和,已知
项和,已知![]() ,且
,且![]() 构成等差数列
构成等差数列
(1)求数列![]() 的通项;
的通项;
(2)令![]() 求数列
求数列![]() 的前
的前![]() 项和
项和![]() .
.
【答案】(1)![]() (2)
(2)![]()
【解析】
(1)依题意,利用等差数列的性质,解关于a2的方程可得a2=2,设数列{an}的公比为q,
继而可求得q1=2,从而可得数列{an}的通项公式;(2)由(1)知an=2n﹣1,依题意知bn=2n﹣1log22n=n2n-1,利用错位相减法即可求得数列{bn}的前n项和Tn.
(1)由已知得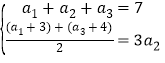 解得a2=2.
解得a2=2.
设数列{an}的公比为q,由a2=2,可得a1=![]() ,a3=2q.
,a3=2q.
又S3=7,可知![]() +2+2q=7,即2q2﹣5q+2=0,
+2+2q=7,即2q2﹣5q+2=0,
解得q1=2,q2=![]() .由题意得q>1,
.由题意得q>1,
∴q=2,∴a1=1,∴an=2n﹣1.
(2)由(1)知,bn=2n﹣1log22n=n2n-1,
故Tn=(1![]() +221+322+…+n2n-1),
+221+322+…+n2n-1),
2Tn=121+222+323…+(n﹣1)2n-1+n2n),
两式相减,可得﹣Tn=(1+2+22+23+…+2n-1﹣n2n)
=![]() ﹣n2n
﹣n2n
=2n﹣1﹣n2n,
∴Tn=![]() .
.


科目:高中数学 来源: 题型:
【题目】伴随着智能手机的深入普及,支付形式日渐多样化,打破了传统支付的局限性和壁垒,有研究表明手机支付的使用比例与人的年龄存在一定的关系,某调研机构随机抽取了50人,对他们一个月内使用手机支付的情况进行了统计,如下表:

(1)若以“年龄55岁为分界点”,由以上统计数据完成下面的![]() 列联表,并判断是否有
列联表,并判断是否有![]() 的把握认为“使用手机支付”与人的年龄有关;
的把握认为“使用手机支付”与人的年龄有关;

(2)若从年龄在![]() ,
,![]() 内的被调查人中各随机选取2人进行追踪调查,记选中的4人中“使用手机支付”的人数为
内的被调查人中各随机选取2人进行追踪调查,记选中的4人中“使用手机支付”的人数为![]() .
.
①求随机变量![]() 的分布列;
的分布列;
②求随机变量![]() 的数学期望.
的数学期望.
参考数据如下:
| 0.05 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
参考格式:![]() ,其中
,其中![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】共享单车因绿色、环保、健康的出行方式,在国内得到迅速推广.最近,某机构在某地区随机采访了10名男士和10名女士,结果男士、女士中分别有7人、6人表示“经常骑共享单车出行”,其他人表示“较少或不选择骑共享单车出行”.
(1)从这些男士和女士中各抽取一人,求至少有一人“经常骑共享单车出行”的概率;
(2)从这些男士中抽取一人,女士中抽取两人,记这三人中“经常骑共享单车出行”的人数为![]() ,求
,求![]() 的分布列与数学期望.
的分布列与数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]()
![]() 的长轴长是短轴长的2倍,且过点
的长轴长是短轴长的2倍,且过点![]() .
.
⑴求椭圆![]() 的方程;
的方程;
⑵若在椭圆上有相异的两点![]() (
(![]() 三点不共线),
三点不共线),![]() 为坐标原点,且直线
为坐标原点,且直线![]() ,直线
,直线![]() ,直线
,直线![]() 的斜率满足
的斜率满足![]() .
.
(ⅰ)求证: ![]() 是定值;
是定值;
(ⅱ)设![]() 的面积为
的面积为![]() ,当
,当![]() 取得最大值时,求直线
取得最大值时,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆M:![]() 与
与![]() 轴相切.
轴相切.
(1)求![]() 的值;
的值;
(2)求圆M在![]() 轴上截得的弦长;
轴上截得的弦长;
(3)若点![]() 是直线
是直线![]() 上的动点,过点
上的动点,过点![]() 作直线
作直线![]() 与圆M相切,
与圆M相切,![]() 为切点,求四边形
为切点,求四边形![]() 面积的最小值.
面积的最小值.
【答案】(1) ![]() (2)
(2) ![]() (3)
(3) ![]()
【解析】试题分析:(1)先将圆的一般方程化成标准方程,利用直线和圆相切进行求解;(2) 令![]() ,得到关于
,得到关于![]() 的一元二次方程进行求解;(3)将四边形的面积的最小值问题转化为点到直线的的距离进行求解.
的一元二次方程进行求解;(3)将四边形的面积的最小值问题转化为点到直线的的距离进行求解.
试题解析:(1) ![]() ∵圆M:
∵圆M:![]() 与
与![]() 轴相切
轴相切
∴![]() ∴
∴![]()
(2) 令![]() ,则
,则![]() ∴
∴![]()
∴![]()
(3) ![]()
∵![]() 的最小值等于点
的最小值等于点![]() 到直线
到直线![]() 的距离,
的距离,
∴![]() ∴
∴![]()
∴四边形![]() 面积的最小值为
面积的最小值为![]() .
.
【题型】解答题
【结束】
20
【题目】在平面直角坐标系![]() 中,圆
中,圆![]() 的方程为
的方程为![]() ,且圆
,且圆![]() 与
与![]() 轴交于
轴交于![]() ,
, ![]() 两点,设直线
两点,设直线![]() 的方程为
的方程为![]() .
.
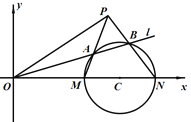
(1)当直线![]() 与圆
与圆![]() 相切时,求直线
相切时,求直线![]() 的方程;
的方程;
(2)已知直线![]() 与圆
与圆![]() 相交于
相交于![]() ,
, ![]() 两点.
两点.
(ⅰ)若![]() ,求实数
,求实数![]() 的取值范围;
的取值范围;
(ⅱ)直线![]() 与直线
与直线![]() 相交于点
相交于点![]() ,直线
,直线![]() ,直线
,直线![]() ,直线
,直线![]() 的斜率分别为
的斜率分别为![]() ,
, ![]() ,
, ![]() ,
,
是否存在常数![]() ,使得
,使得![]() 恒成立?若存在,求出
恒成立?若存在,求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数![]() 的图象为
的图象为![]() ,则以下结论中正确的是__________.(写出所有正确结论的编号)
,则以下结论中正确的是__________.(写出所有正确结论的编号)
①图象![]() 关于直线
关于直线![]() 对称;
对称;
②图象![]() 关于点
关于点![]() 对称;
对称;
③函数![]() 在区间
在区间![]() 内是增函数;
内是增函数;
④由![]() 的图象向右平移
的图象向右平移![]() 个单位长度可以得到图象
个单位长度可以得到图象![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(Ⅰ)求函数![]() 的单调区间;
的单调区间;
(Ⅱ)如果对于任意的![]() ,
,![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(III)设函数![]() ,
, ![]() ,过点
,过点![]() 作函数
作函数![]() 的图象的所有切线,令各切点的横坐标按从小到大构成数列
的图象的所有切线,令各切点的横坐标按从小到大构成数列![]() ,求数列
,求数列![]() 的所有项之和的值.
的所有项之和的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△![]() 中,角
中,角![]() 、
、![]() 、
、![]() 所对的边分别为
所对的边分别为![]() 、
、![]() 、
、![]() ,给出四个命题:
,给出四个命题:
(1)若![]() ,则△
,则△![]() 为等腰三角形;
为等腰三角形;
(2)若![]() ,则△
,则△![]() 为直角三角形;
为直角三角形;
(3)若![]() ,则△
,则△![]() 为等腰直角三角形;
为等腰直角三角形;
(4)若![]() ,则△
,则△![]() 为正三角形;
为正三角形;
以上正确命题的个数是( )
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com