
分析 利用面积求出角B,再利用余弦定理求出AC,即可求出角C.
解答 解:由s=$\frac{1}{2}AB•AC•sinB$=$\frac{3-\sqrt{3}}{2}$,可得sinB=$\frac{\sqrt{3}}{2}$,
∵∠B为钝角,∴B=$\frac{2π}{3}$.
在△ABC中,由余弦定理得:AC2=AB2+CB2-2AB•CB•cosB,⇒AC=$\sqrt{6}$,
由正弦定理得$\frac{AB}{sinC}=\frac{AC}{sinB}$,解得sinC=$\frac{\sqrt{2}}{2}$,
∵C为锐角,∴C=45°.
故答案为:450
点评 本题考查了正余弦定理的应用,属于中档题.


 智能训练练测考系列答案
智能训练练测考系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
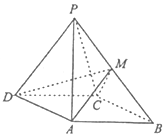 如图,四棱锥P-ABCD中,侧面PDC是正三角形,底面ABCD是边长为2$\sqrt{3}$的菱形,∠DAB=120°,且侧面PDC与底面垂直,M为PB的中点.
如图,四棱锥P-ABCD中,侧面PDC是正三角形,底面ABCD是边长为2$\sqrt{3}$的菱形,∠DAB=120°,且侧面PDC与底面垂直,M为PB的中点.查看答案和解析>>
科目:高中数学 来源:2016-2017学年河北省高二理上第一次月考数学试卷(解析版) 题型:选择题
在棱长为3的正方体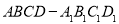 中,
中, 在线段
在线段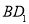 上,且
上,且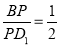 ,
,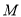 为线段
为线段 上的动点,则三棱锥
上的动点,则三棱锥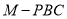 的体积为( )
的体积为( )
A.1 B.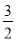
C.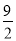 D.与
D.与 点的位置有关
点的位置有关
查看答案和解析>>
科目:高中数学 来源:2015-2016学年四川省高二上学期期中考数学试卷(解析版) 题型:填空题
已知直线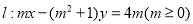 和圆
和圆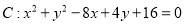 .有以下几个结论:
.有以下几个结论:
①直线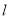 的倾斜角不是钝角;
的倾斜角不是钝角;
②直线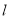 必过第一、三、四象限;
必过第一、三、四象限;
③直线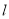 能将圆
能将圆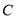 分割成弧长的比值为
分割成弧长的比值为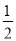 的两段圆弧;
的两段圆弧;
④直线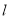 与圆
与圆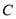 相交的最大弦长为
相交的最大弦长为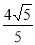 .
.
其中正确的是________________.(写出所有正确说法的番号).
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -16 | B. | 8 | C. | 16 | D. | 24 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com