
| A. | -16 | B. | 8 | C. | 16 | D. | 24 |
分析 由题意可知G为AB的中点,于是${(\overrightarrow{OA}-\overrightarrow{OB})^2}-4{\overrightarrow{OG}^2}$=-4$\overrightarrow{OA}•\overrightarrow{OB}$,设A(x1,$\frac{{{x}_{1}}^{2}}{4}$),B(x2,$\frac{{{y}_{2}}^{2}}{4}$),得出$\overrightarrow{OA}•\overrightarrow{OB}$关于x1x2的函数,从而得出答案.
解答 解:∵$\overrightarrow{AB}=2\overrightarrow{AG}$,∴G是AB的中点,
∴$\overrightarrow{OG}$=$\frac{1}{2}$($\overrightarrow{OA}+\overrightarrow{OB}$),
∴${(\overrightarrow{OA}-\overrightarrow{OB})^2}-4{\overrightarrow{OG}^2}$=($\overrightarrow{OA}-\overrightarrow{OB}$)2-($\overrightarrow{OA}+\overrightarrow{OB}$)2=-4$\overrightarrow{OA}•\overrightarrow{OB}$,
设A(x1,$\frac{{{x}_{1}}^{2}}{4}$),B(x2,$\frac{{{y}_{2}}^{2}}{4}$),
则$\overrightarrow{OA}•\overrightarrow{OB}$=x1x2+($\frac{{x}_{1}{x}_{2}}{4}$)2=($\frac{{x}_{1}{x}_{2}}{4}$+2)2-4≥-4,
∴-4$\overrightarrow{OA}•\overrightarrow{OB}$≤16,即${(\overrightarrow{OA}-\overrightarrow{OB})^2}-4{\overrightarrow{OG}^2}$的最大值为16.
故选C.
点评 本题考查了平面向量的数量积运算,抛物线的定义,属于中档题.


 备战中考寒假系列答案
备战中考寒假系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源:2015-2016学年四川省高二上学期期中考数学试卷(解析版) 题型:选择题
不等式 的解集是( )
的解集是( )
A.(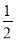 ,+
,+ )
)
B.(4,+ )
)
C.(﹣ ,﹣3)∪(4,+
,﹣3)∪(4,+ )
)
D.(﹣ ,﹣3)∪(
,﹣3)∪(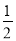 ,+
,+ )
)
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 144 | B. | 288 | C. | 216 | D. | 360 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | $\frac{11}{3}$ | C. | $\frac{10}{3}$ | D. | $\frac{8}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com