
分析 (1)先求出曲线C的普通方程,由此能求出曲线C的极坐标方程;把直线l的参数方程化为普通方程,由此能求出直线l的极坐标方程.
(2)联立$\left\{\begin{array}{l}{(x-2)^{2}+(y-1)^{2}=9}\\{x+y=0}\end{array}\right.$,求出曲线C和直线l的交点的直角坐标,由此能求出曲线C和直线l的交点的极坐标.
解答 解:(1)∵曲线C的参数方程为$\left\{\begin{array}{l}{x=2+3cosα}\\{y=1+3sinα}\end{array}\right.$(α为参数),
∴曲线C的普通方程为(x-2)2+(y-1)2=9,
即x2+y2-4x-2y=4,
∴曲线C的极坐标方程为ρ2-4ρcosθ-2ρsinθ=4,
即ρ2-2ρ(2cosθ+sinθ)=4.
∵直线l的参数方程为$\left\{\begin{array}{l}{x=t}\\{y=-t}\end{array}\right.$(t为参数),
∴直线l的普通方程为x+y=0,
∴直线l的极坐标方程为ρcosθ+ρsinθ=0,即ρ(cosθ+sinθ)=0.
(2)联立$\left\{\begin{array}{l}{(x-2)^{2}+(y-1)^{2}=9}\\{x+y=0}\end{array}\right.$,得$\left\{\begin{array}{l}{x=-1}\\{y=1}\end{array}\right.$或$\left\{\begin{array}{l}{x=2}\\{y=-2}\end{array}\right.$,
∴曲线C和直线l的交点的直角坐标为(-1,1)或(2,-2),
∴曲线C和直线l的交点的极坐标为($\sqrt{2}$,$\frac{3π}{4}$),(2$\sqrt{2}$,$\frac{7π}{4}$).
点评 本小题主要考查极坐标系与参数方程的相关知识,具体涉及到极坐标方程与平面直角坐标方程的互化,考查推理论证能力、运算求解能力,考查函数与方程思想、化归与转化思想,是中档题.


科目:高中数学 来源:2016-2017学年河北省高二理上第一次月考数学试卷(解析版) 题型:选择题
在棱长为3的正方体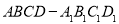 中,
中, 在线段
在线段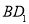 上,且
上,且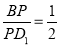 ,
,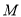 为线段
为线段 上的动点,则三棱锥
上的动点,则三棱锥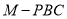 的体积为( )
的体积为( )
A.1 B.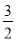
C.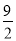 D.与
D.与 点的位置有关
点的位置有关
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -16 | B. | 8 | C. | 16 | D. | 24 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 命题“若a>1,则a2>1”的否命题为:“若a>1,则a2≤1” | |
| B. | 命题“?x0>1,使得-x02+2x0-1≥0”的否定“?x≤1,使得-x2+2x-1<0” | |
| C. | “x>-1”是“$\frac{1}{x}<-1$”成立的必要不充分条件 | |
| D. | 正弦函数是奇函数,f(x)=sin(x2+1)是正弦函数,所以f(x)=sin(x2+1)是奇函数,上述推理错误的原因是大前提不正确 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 2$\sqrt{2}$ | C. | 2 | D. | $\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com