
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
分析 求函数的导数,由题意可得a2、a4030是对应方程的实根,由韦达定理可得a2+a4030的值,然后由等差数列的性质可得a2016的值,代入化简即可.
解答 解:∵$f(x)=\frac{1}{3}{x^3}-4{x^2}+6x-1$,
∴f′(x)=x2-8x+6,
∵等差数列{an}中的a2、a4030是函数$f(x)=\frac{1}{3}{x^3}-4{x^2}+6x-1$的两个极值点,
∴a2+a4030=8,∴${a}_{2016}=\frac{1}{2}({a}_{2}+{a}_{4030})=\frac{1}{2}×8=4$,
∴log2(a2016)=log24=2.
故选:A.
点评 本题考查等差数列的性质和韦达定理,属基础题,解题时要认真审题,注意等差数列的性质、导数知识的合理运用.


 灵星计算小达人系列答案
灵星计算小达人系列答案科目:高中数学 来源:2015-2016学年四川省高二上学期期中考数学试卷(解析版) 题型:选择题
不等式 的解集是( )
的解集是( )
A.(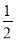 ,+
,+ )
)
B.(4,+ )
)
C.(﹣ ,﹣3)∪(4,+
,﹣3)∪(4,+ )
)
D.(﹣ ,﹣3)∪(
,﹣3)∪(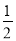 ,+
,+ )
)
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | $\frac{11}{3}$ | C. | $\frac{10}{3}$ | D. | $\frac{8}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①② | B. | ②③ | C. | ①③ | D. | ③④ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com