
分析 (Ⅰ)由曲线C1的极坐标方程能求出曲线C1的直角坐标方程;曲线C2的参数方程消去参数,能求出C2的普通方程.
(Ⅱ)由已知得$ρ_1^2=\frac{4}{{1+3{{sin}^2}{θ_0}}}$,$ρ_2^2=\frac{4}{{1+3{{sin}^2}({θ_0}+\frac{π}{2})}}$,由此能求出$\frac{1}{ρ_1^2}$+$\frac{1}{ρ_2^2}$的值.
解答 (本小题满分10分)
解:(Ⅰ)∵曲线C1的极坐标方程为ρ2(1+3sin2θ)=4,
∴ρ2+3ρ2sin2θ=4,
∴曲线C1的直角坐标方程${C_1}:\frac{x^2}{4}+{y^2}=1$,
∵曲线C2:$\left\{\begin{array}{l}{x=2+2cosθ}\\{y=2sinθ}\end{array}$(θ为参数).
∴C2的普通方程${C_2}:{(x-2)^2}+{y^2}=4$.(5分)
(Ⅱ)∵A(ρ1,θ0),B(ρ2,θ0+$\frac{π}{2}$)都在曲线C1上,
∴$ρ_1^2=\frac{4}{{1+3{{sin}^2}{θ_0}}}$,$ρ_2^2=\frac{4}{{1+3{{sin}^2}({θ_0}+\frac{π}{2})}}$,
$\frac{1}{ρ_1^2}=\frac{{1+3{{sin}^2}{θ_0}}}{4}$,$\frac{1}{ρ_2^2}=\frac{{1+3{{cos}^2}{θ_0}}}{4}$,
∴$\frac{1}{ρ_1^2}+\frac{1}{ρ_2^2}=\frac{{1+3{{sin}^2}{θ_0}}}{4}+\frac{{1+3{{cos}^2}{θ_0}}}{4}=\frac{5}{4}$.(10分)
点评 本题主要考查极坐标系与参数方程的相关知识,具体涉及到极坐标方程与平面直角坐标方程的互化,考查推理论证能力、运算求解能力,考查函数与方程思想、化归与转化思想,是中档题.


 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:高中数学 来源: 题型:解答题
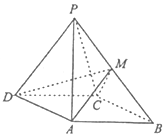 如图,四棱锥P-ABCD中,侧面PDC是正三角形,底面ABCD是边长为2$\sqrt{3}$的菱形,∠DAB=120°,且侧面PDC与底面垂直,M为PB的中点.
如图,四棱锥P-ABCD中,侧面PDC是正三角形,底面ABCD是边长为2$\sqrt{3}$的菱形,∠DAB=120°,且侧面PDC与底面垂直,M为PB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 下边程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”,执行该程序框图时,若输入a,b分别为18,27,则输出的a=( )
下边程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”,执行该程序框图时,若输入a,b分别为18,27,则输出的a=( )| A. | 0 | B. | 9 | C. | 18 | D. | 54 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -16 | B. | 8 | C. | 16 | D. | 24 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 命题“若a>1,则a2>1”的否命题为:“若a>1,则a2≤1” | |
| B. | 命题“?x0>1,使得-x02+2x0-1≥0”的否定“?x≤1,使得-x2+2x-1<0” | |
| C. | “x>-1”是“$\frac{1}{x}<-1$”成立的必要不充分条件 | |
| D. | 正弦函数是奇函数,f(x)=sin(x2+1)是正弦函数,所以f(x)=sin(x2+1)是奇函数,上述推理错误的原因是大前提不正确 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
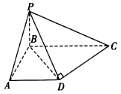 如图,在四棱锥P-ABCD中,已知PB⊥底面ABCD,BC⊥AB,AD∥BC,AB=AD=2,CD⊥PD,异面直线PA与CD所成角等于60°.
如图,在四棱锥P-ABCD中,已知PB⊥底面ABCD,BC⊥AB,AD∥BC,AB=AD=2,CD⊥PD,异面直线PA与CD所成角等于60°.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com