
分析 对2-a,2+a与2的大小关系分类讨论,即可得出.
解答 解:①当2-a<2,2+a<2时,此时a不存在,舍去;
②当2-a≥2,2+a≥2时,此时a=0,舍去;
③当2-a≥2,2+a<2时,a≠0,此时a<0,-(2-a)-a=2(2+a)+3a,解得a=-$\frac{6}{5}$.
④当2-a<2,2+a≥2时,a≠0,此时a>0,由f(2-a)=f(2+a),可得:2(2-a)+3a=-(2+a)-a,解得a=-2,舍去.
综上可得:a=-$\frac{6}{5}$.
故答案为:-$\frac{6}{5}$.
点评 本题考查了函数的值、分类讨论方法,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
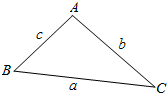 (1)如图所示.在△ABC中,射影定理可表示为a=b•cosC+c•cosB.其中a,b,c分别为角A,B,C的对边,类比上述定理.写出对空间四面体性质的猜想.
(1)如图所示.在△ABC中,射影定理可表示为a=b•cosC+c•cosB.其中a,b,c分别为角A,B,C的对边,类比上述定理.写出对空间四面体性质的猜想.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=$\frac{1}{x}$ | B. | y=-tanx | C. | y=log${\;}_{\frac{1}{2}}$x | D. | y=$\frac{1}{{2}^{x}}-{2}^{x}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
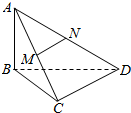 如图所示,已知AB⊥平面BCD,M,N分别是AC,AD的中点,BC⊥CD.
如图所示,已知AB⊥平面BCD,M,N分别是AC,AD的中点,BC⊥CD.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com