
| A. | $\frac{{e-\sqrt{{e^2}-1}}}{e}$ | B. | $\frac{{2\sqrt{{e^2}+1}-e}}{2e}$ | C. | $\frac{{\sqrt{{e^2}+1}-e}}{2e}$ | D. | $e+\frac{1}{e}-\frac{1}{2}$ |
分析 由圆的对称性可得只需考虑圆心C(e+$\frac{1}{e}$,0)到函数f(x)=lnx图象上一点的距离的最小值.设f(x)图象上一点P(m,lnm),求得切线的斜率,由两直线垂直的条件:斜率之积为-1,可得lnm+m2-(e+$\frac{1}{e}$)m=0,由g(x)=lnx+x2-(e+$\frac{1}{e}$)x,求出导数,判断单调性,可得零点e,运用两点的距离公式计算即可得到所求值
解答 解:由圆的对称性可得只需考虑圆心C(e+$\frac{1}{e}$,0)到函数f(x)=lnx图象上一点的距离的最小值.
设f(x)图象上一点(m,lnm),
由f(x)的导数为f′(x)=$\frac{1}{x}$,即有切线的斜率为k=$\frac{1}{m}$,
可得$\frac{lnm-0}{m-(e+\frac{1}{e})}$=-m,
即有lnm+m2-(e+$\frac{1}{e}$)m=0,
由g(x)=lnx+x2-(e+$\frac{1}{e}$)x,可得g′(x)=$\frac{1}{x}$+2x-(e+$\frac{1}{e}$),
当2<x<3时,g′(x)>0,g(x)递增.
又g(e)=lne+e2-(e+$\frac{1}{e}$)•e=0,
可得x=e处点P(e,1)到点Q的距离最小,且为$\sqrt{1+\frac{1}{{e}^{2}}}$,
则线段PQ的长度的最小值为$\sqrt{1+\frac{1}{{e}^{2}}}$-$\frac{1}{2}$=$\frac{2\sqrt{{e}^{2}+1}-e}{2e}$.
故选:B.
点评 本题考查导数的运用:求切线的斜率和单调性,考查圆的对称性和两点的距离公式,考查运算能力,属于中档题.


 同步拓展阅读系列答案
同步拓展阅读系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{5π}{2}$ | B. | $\frac{5π}{4}$ | C. | $\frac{3+π}{2}$ | D. | 3+π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 做米饭需要刷锅,淘米,添水,加热这些步骤 | |
| B. | 洗衣机的使用说明书 | |
| C. | 利用公式S=πr2计算半径为4的圆的面积,就是计算π×42 | |
| D. | 解方程2x2+x-1=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
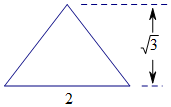 一个四棱锥的侧棱长都相等,底面是正方形,且其正视图为如图所示的等腰三角形,则该四棱锥的体积是( )
一个四棱锥的侧棱长都相等,底面是正方形,且其正视图为如图所示的等腰三角形,则该四棱锥的体积是( )| A. | $\frac{{4\sqrt{3}}}{3}$ | B. | $2\sqrt{3}$ | C. | $4\sqrt{3}$ | D. | $\frac{8}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $y=x+\frac{4}{x}$ | B. | $y=sinx+\frac{4}{sinx}(0<x<π)$ | ||
| C. | y=4log3x+logx3 | D. | y=4ex+e-x |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com