
| A. | -6 | B. | 6 | C. | $\frac{8}{3}$ | D. | -$\frac{8}{3}$ |
分析 把m=4-xi,n=3+2i代入$\frac{n}{m}$,然后由复数代数形式的乘除运算化简,再结合已知条件求解即可得答案.
解答 解:由m=4-xi,n=3+2i,
得$\frac{n}{m}=\frac{3+2i}{4-xi}=\frac{(3+2i)(4+xi)}{(4-xi)(4+xi)}$=$\frac{12-2x+(8+3x)i}{16+{x}^{2}}$=$\frac{12-2x}{16+{x}^{2}}+\frac{8+3x}{16+{x}^{2}}i$,
∵复数$\frac{n}{m}$∈R,
∴$\frac{8+3x}{16+{x}^{2}}=0$,解得x=$-\frac{8}{3}$.
故选:D.
点评 本题考查了复数代数形式的乘除运算,考查了复数的基本概念,是基础题.


 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案科目:高中数学 来源: 题型:解答题
| A类 | B类 | C类 | |
| 男生 | 18 | x | 3 |
| 女生 | 10 | 8 | y |
| 男生 | 女生 | 总计 | |
| A类 | |||
| B类和C类 | |||
| 总计 |
| P(K2≥k0) | 0.10 | 0.05 | 0.01 |
| k0 | 2.706 | 3.841 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
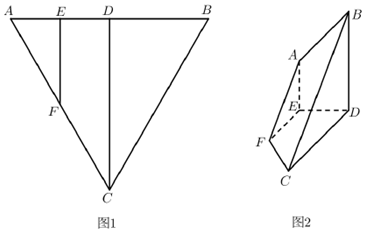
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{7}{4}$ | B. | $\frac{7}{5}$ | C. | $\frac{8}{5}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | 2 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
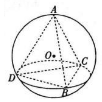 体积为$18\sqrt{3}$的正三棱锥A-BCD的每个顶点都在半径为R的球O的球面上,球心O在此三棱锥内部,且R:BC=2:3,点E为线段BD上一点,且DE=2EB,过点E作球O的截面,则所得截面圆面积的取值范围是( )
体积为$18\sqrt{3}$的正三棱锥A-BCD的每个顶点都在半径为R的球O的球面上,球心O在此三棱锥内部,且R:BC=2:3,点E为线段BD上一点,且DE=2EB,过点E作球O的截面,则所得截面圆面积的取值范围是( )| A. | [4π,12π] | B. | [8π,16π] | C. | [8π,12π] | D. | [12π,16π] |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com