
分析 ($\frac{2}{x}$+x+1)(1-2$\sqrt{x}$+x)4=($\frac{2}{x}$+x+1)$(\sqrt{x}-1)^{8}$.$(\sqrt{x}-1)^{8}$的展开式的通项公式:Tr+1=${∁}_{8}^{r}$(-1)8-r$(\sqrt{x})^{r}$=${∁}_{8}^{r}$(-1)8-r${x}^{\frac{r}{2}}$.令$\frac{r}{2}$=2,0,1,分别解得r,进而得出.
解答 解:($\frac{2}{x}$+x+1)(1-2$\sqrt{x}$+x)4=($\frac{2}{x}$+x+1)$(\sqrt{x}-1)^{8}$.
$(\sqrt{x}-1)^{8}$的展开式的通项公式:Tr+1=${∁}_{8}^{r}$(-1)8-r$(\sqrt{x})^{r}$=${∁}_{8}^{r}$(-1)8-r${x}^{\frac{r}{2}}$.
令$\frac{r}{2}$=2,0,1,分别解得r=4,0,2.
∴($\frac{2}{x}$+x+1)(1-2$\sqrt{x}$+x)4的展开式中x的系数=2×${∁}_{8}^{4}×(-1)^{4}$+${∁}_{8}^{0}$(-1)8+${∁}_{8}^{2}(-1)^{6}$=169.
故答案为:169.
点评 本题考查了二项式定理的通项公式及其性质,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | b>c>a | B. | b>a>c | C. | a>c>b | D. | a>b>c |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{1}{3}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | -$\frac{2}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
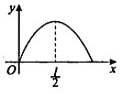 动点P从点A出发,按逆时针方向沿周长为1的平面图形运动一周,A,P两点间的距离y与动点P所走过的路程x的关系如图所示,那么动点P所走的图形可能是( )
动点P从点A出发,按逆时针方向沿周长为1的平面图形运动一周,A,P两点间的距离y与动点P所走过的路程x的关系如图所示,那么动点P所走的图形可能是( )| A. | 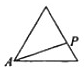 | B. | 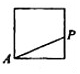 | C. | 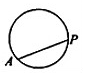 | D. | 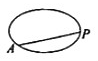 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -6 | B. | 6 | C. | $\frac{8}{3}$ | D. | -$\frac{8}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
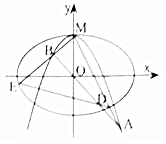 如图,抛物线C1:y=b-x2经过椭圆C2:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的焦点及上顶点M,过点M的两条互相垂直的直线l1,l2分别交抛物线于A,B两点,交椭圆于D,E两点,已知抛物线C1:y=b-x2与x轴所围成的区域面积为$\frac{4}{3}$.
如图,抛物线C1:y=b-x2经过椭圆C2:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的焦点及上顶点M,过点M的两条互相垂直的直线l1,l2分别交抛物线于A,B两点,交椭圆于D,E两点,已知抛物线C1:y=b-x2与x轴所围成的区域面积为$\frac{4}{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 8 | C. | 16 | D. | 32 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com