
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 对于①,分a>b≥0、a≥0>b、0>a>b三类讨论,可判断①正确;
对于②,在△ABC中,利用正弦定理可判断②正确;
对于③,非零向量$\overrightarrow a,\overrightarrow b$,若$\overrightarrow a•\overrightarrow b>0$⇒向量$\overrightarrow a$与向量$\overrightarrow b$的夹角为锐角或0,可判断③错误;
对于④,利用作差法可判断$\frac{ln3}{3}$-$\frac{ln2}{2}$=$\frac{ln9-ln8}{6}$>0,即$\frac{ln3}{3}$>$\frac{ln2}{2}$;同理可得,$\frac{ln2}{2}>\frac{ln5}{5}$,可判断④正确.
解答 解:对于①,若a>b≥0,则a|a|>b|b|显然成立;
若a≥0>b,a|a|>b|b|?a2>-b2?a2+b2>0,成立;
若0>a>b,a|a|>b|b||?-a2>-b2?a2<b2,成立;
故对任意的a,b∈R,a>b是a|a|>b|b|的充要条件,故①正确;
对于②,在△ABC中,若A>B,则a>b,又由正弦定理知,a>b?2RsinA>2RsinB?sinA>sinB,故②正确;
对于③,非零向量$\overrightarrow a,\overrightarrow b$,若$\overrightarrow a•\overrightarrow b>0$,则向量$\overrightarrow a$与向量$\overrightarrow b$的夹角为锐角或0,故③错误;
对于④,∵$\frac{ln3}{3}$-$\frac{ln2}{2}$=$\frac{2ln3-3ln2}{6}$=$\frac{ln9-ln8}{6}$>0,
∴$\frac{ln3}{3}$>$\frac{ln2}{2}$;
同理可得,$\frac{ln2}{2}>\frac{ln5}{5}$;
∴$\frac{ln3}{3}>\frac{ln2}{2}>\frac{ln5}{5}$,故④正确.
综上所述,真命题的个数为3个,
故选:C.
点评 本题考查命题的真假判断与应用,考查充分必要条件、正弦定理、向量的数量积及对数的运算性质,考查分类讨论思想、等价转化思想的综合运用,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{{\sqrt{3}}}{3}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
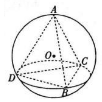 体积为$18\sqrt{3}$的正三棱锥A-BCD的每个顶点都在半径为R的球O的球面上,球心O在此三棱锥内部,且R:BC=2:3,点E为线段BD上一点,且DE=2EB,过点E作球O的截面,则所得截面圆面积的取值范围是( )
体积为$18\sqrt{3}$的正三棱锥A-BCD的每个顶点都在半径为R的球O的球面上,球心O在此三棱锥内部,且R:BC=2:3,点E为线段BD上一点,且DE=2EB,过点E作球O的截面,则所得截面圆面积的取值范围是( )| A. | [4π,12π] | B. | [8π,16π] | C. | [8π,12π] | D. | [12π,16π] |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com