
在平面直角坐标系xoy中,已知椭圆C: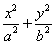 =1(a>b≥1)的离心率e=
=1(a>b≥1)的离心率e=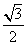 ,且椭圆C上的点到点Q (0,3)的距离最大值为4,过点M(3,0)的直线交椭圆C于点A、B.
,且椭圆C上的点到点Q (0,3)的距离最大值为4,过点M(3,0)的直线交椭圆C于点A、B.
(I)求椭圆C的方程。
(II)设P为椭圆上一点,且满足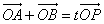 (O为坐标原点),当|AB|<
(O为坐标原点),当|AB|<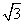 时,求实数t的取值范围.
时,求实数t的取值范围.
科目:高中数学 来源: 题型:
某商场对A品牌的商品进行了市场调查,预计2012年从1月起前x个月顾客对A品牌的商品的需求总量P(x)件与月份x的近似关系是:
P(x)= x(x+1)(41-2x)(x≤12且x∈N*)
x(x+1)(41-2x)(x≤12且x∈N*)
(1)写出第x月的需求量f(x)的表达式;
(2)若第x月的销售量g(x)=

(单位:件),每件利润q(x)元与月份x的近似关系为:q(x)=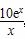 ,问:该商场销售A品牌商品,预计第几月的月利润达到最大值?月利润最大值是多少?(e6≈403)
,问:该商场销售A品牌商品,预计第几月的月利润达到最大值?月利润最大值是多少?(e6≈403)
查看答案和解析>>
科目:高中数学 来源: 题型:
一个几何体的三视图如图所示(单位长度:cm),则此几何体的表面积是( )
A.(20+4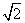 )cm2 B. 21 cm2 C.(24+4
)cm2 B. 21 cm2 C.(24+4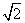 )cm2 D. 24 cm2
)cm2 D. 24 cm2

查看答案和解析>>
科目:高中数学 来源: 题型:
设f(x)是定义在R上的偶函数,且当x≥0时,f(x)=(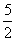 )x,若对任意的x∈[a, a+l],
)x,若对任意的x∈[a, a+l],
不等式f(x+a)≥f2(x)恒成立,则实数a的取值范围是____ 。
查看答案和解析>>
科目:高中数学 来源: 题型:
某研究机构对高三学生的记忆力x和判断力y进行统计分析,得下表数据:
| x | 6 | 8 | 10 | 12 |
| y | 2 | 3 | 5 | 6 |
根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程 中的
中的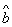 的值为
的值为 ,则记忆力为14的同学的判断力约为(附:线性回归方程
,则记忆力为14的同学的判断力约为(附:线性回归方程 中,
中, ,
,
其中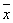 ,
, 为样本平均值)
为样本平均值)
A.7 B. C.8 D.
C.8 D.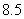
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com